已知函数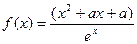 ,(
,(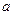 为常数,
为常数,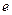 为自然对数的底).
为自然对数的底).
(1)令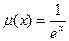 ,
,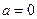 ,求
,求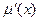 和
和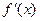 ;
;
(2)若函数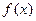 在
在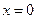 时取得极小值,试确定
时取得极小值,试确定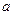 的取值范围;
的取值范围;
[理](3)在(2)的条件下,设由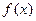 的极大值构成的函数为
的极大值构成的函数为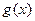 ,试判断曲线
,试判断曲线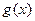 只可能与直线
只可能与直线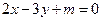 、
、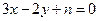 (
(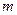 ,
,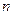 为确定的常数)中的哪一条相切,并说明理由.
为确定的常数)中的哪一条相切,并说明理由.
(本小题满分12分)己知函数 ,
,
(1)求函数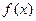 的单调区间;
的单调区间;
(2)当 时,证明:对
时,证明:对 时,不等式
时,不等式 成立;
成立;
(3)当 ,
, 时,证明:
时,证明: .
.
(本小题满分12分)已知抛物线 :
: (
(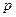 为正常数)的焦点为
为正常数)的焦点为 ,过
,过 做一直线
做一直线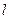 交抛物线
交抛物线 于
于
 ,
,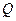 两点,点
两点,点 为坐标原点.
为坐标原点.
(1)若 的面积记为
的面积记为 ,求
,求 的值;
的值;
(2)若直线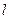 垂直于
垂直于 轴,过点P做关于直线
轴,过点P做关于直线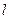 对称的两条直线
对称的两条直线 ,
, 分别交抛物线C于M,N两点,证明:直线MN斜率等于抛物线在点Q处的切线斜率.
分别交抛物线C于M,N两点,证明:直线MN斜率等于抛物线在点Q处的切线斜率.
(本小题满分12分)
己知三棱 柱
柱 ,
, 在底面ABC上的射影恰为AC的中点D,
在底面ABC上的射影恰为AC的中点D, ,
,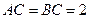 ,又知
,又知

(1)求证: 平面
平面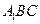 ;
;
(2)求点C到平面 的距离;
的距离;
(3)求二面角 余弦值的大小.
余弦值的大小.
(本小题满分12分)
在清明节前,哈市某单位组织员工参加植树祭扫,林管局在植树前为了保证树苗质量,都会对树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗的高度,量出它们的高度如下:(单位:厘米)
甲:37 21 31 21 28 19 32 23 25 33
乙:10 30 47 27 46 14 26 11 43 46
(1)根据抽测结果画出茎叶图,并根据你所填写的茎叶图对两种树苗高度作比较,写出3个统计结论;
(2)如果认为甲种树苗高度超过30厘米为优质树苗,那么在己抽测的甲种10株树苗中任选两株栽种,记优质树苗的个数为 ,求
,求 的分布列和期望.
的分布列和期望.
(本小题满分12分)如图,在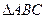 中,
中,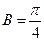 ,
,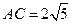 ,
,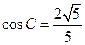

(1)求 ;
;
(2)记BC的中点为D,求中线AD的长.