(本小题满分14分).如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D、E分别在棱PB、PC的中点,且DE∥BC.
(1)求证:DE∥平面ACD
(2)求证:BC⊥平面PAC;
(3)求AD与平面PAC所成的角的正弦值;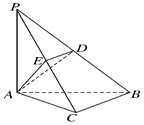
已知数列 的前
的前 项和
项和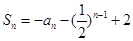
 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)令 ,
,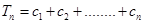 ,试比较
,试比较 与
与 的大小,并予以证明.
的大小,并予以证明.
某大学毕业生响应国家“自主创业”的号召,今年年初组织一些同学自筹资金 万元购进一台设备,并立即投入生产自行设计的产品,计划第一年维修、保养费用
万元购进一台设备,并立即投入生产自行设计的产品,计划第一年维修、保养费用 万元,从第二年开始,每年所需维修、保养费用比上一年增加
万元,从第二年开始,每年所需维修、保养费用比上一年增加 万元,该设备使用后,每年的总收入为
万元,该设备使用后,每年的总收入为 万元,设从今年起使用
万元,设从今年起使用 年后该设备的盈利额为
年后该设备的盈利额为 万元。
万元。
(Ⅰ)写出 的表达式;
的表达式;
(Ⅱ)求从第几年开始,该设备开始盈利;
(Ⅲ)使用若干年后,对该设备的处理方案有两种:方案一:年平均盈利额达到最大值时,以 万元价格处理该设备;方案二:当盈利额达到最大值时,以16万元价格处理该设备。问用哪种方案处理较为合算?请说明理由.
万元价格处理该设备;方案二:当盈利额达到最大值时,以16万元价格处理该设备。问用哪种方案处理较为合算?请说明理由.
已知公差不为零的等差数列 的前
的前 项和
项和 且
且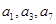 成等比数列.
成等比数列.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 为数列
为数列 的前
的前 项和,若
项和,若
 对任意
对任意 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.
已知函数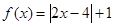 .
.
(Ⅰ)解不等式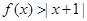 ;
;
(Ⅱ)设正数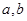 满足
满足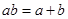 ,若不等式
,若不等式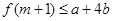 对任意
对任意 都成立,求实数
都成立,求实数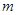 的取值范围.
的取值范围.
已知等比数列 满足2a1+a3=3a2,且a3+2是a2,a4的等差中项.
满足2a1+a3=3a2,且a3+2是a2,a4的等差中项.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若 ,Sn=b1+b2+…+bn,求使Sn-2n+1+47<0成立的正整数n的最小值.
,Sn=b1+b2+…+bn,求使Sn-2n+1+47<0成立的正整数n的最小值.