(本小题满分14分)
已知函数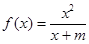 的图像经过点
的图像经过点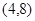 .
.
(1)求该函数的解析式;
(2)数列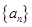 中,若
中,若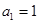 ,
,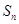 为数列
为数列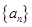 的前
的前 项和,且满足
项和,且满足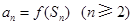 ,
,
证明数列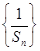 成等差数列,并求数列
成等差数列,并求数列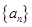 的通项公式;
的通项公式;
(3)另有一新数列 ,若将数列
,若将数列 中的所有项按每一行比上一行多一项的规则排成
中的所有项按每一行比上一行多一项的规则排成
如下数表:
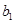 |
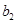 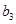 |
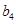 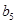 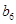 |
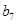 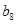 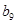 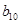 |
记表中的第一列数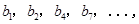 构成的数列即为数列
构成的数列即为数列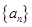 ,上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当
,上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当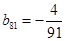 时,求上表中第
时,求上表中第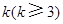 行所有项的和.
行所有项的和.
如图,已知圆上的弧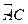 =
=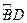 ,过C点的圆的切线与BA的延长线交
,过C点的圆的切线与BA的延长线交 于E点,证明:
于E点,证明:
证明:(Ⅰ)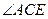 =
=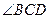 ;(Ⅱ)
;(Ⅱ) ;
;
(12分 )(12分)设a≥0,f(x)=x-1-ln2 x+2a ln x(x>0).
)(12分)设a≥0,f(x)=x-1-ln2 x+2a ln x(x>0).
(Ⅰ)令F(x)=xf'(x),讨论F (x)在(0,+∞)内的单调性并求极值;
(x)在(0,+∞)内的单调性并求极值;
(Ⅱ)求证:当x>1时,恒有x>ln2x -2a ln x+1
-2a ln x+1
轮船A和轮船B在中午12点整离开港口C,两艘轮船的航行方向之间的夹角为 ,轮船A的航行速度为25 千米/小时,轮船B的航行速度是15 千米/小时,下午2时两艘船的距离是多少?
,轮船A的航行速度为25 千米/小时,轮船B的航行速度是15 千米/小时,下午2时两艘船的距离是多少?
已知函数 (其中
(其中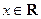 ),求:
),求:
 函数
函数 的最小正周期;
的最小正周期; 函数
函数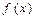 图象的对称轴和对称中心
图象的对称轴和对称中心
(12分) 在ΔABC中,已知 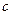 = 4,A = 45°,B = 15°,求a、b、和
= 4,A = 45°,B = 15°,求a、b、和