设函数 ,
,
(1)若函数 在
在 处与直线
处与直线 相切;
相切;
①求实数 的值;②求函数
的值;②求函数 上的最大值;
上的最大值;
(2)当 时,若不等式
时,若不等式 对所有的
对所有的 都成立,求实数
都成立,求实数 的取值范围.
的取值范围.
设曲线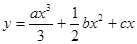 在点
在点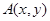 处的切线斜率为
处的切线斜率为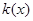 ,且
,且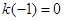 .对一切实数
.对一切实数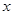 ,不等式
,不等式 恒成立(
恒成立(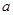 ≠0).
≠0).
(1) 求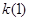 的值;
的值;
(2) 求函数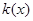 的表达式;
的表达式;
(3) 求证: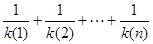 >
>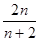 .
.
哈六中体育节进行定点投篮游戏,已知参加游戏的甲、乙两人,他们每一次投篮投中的概率均为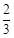 ,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
(1)求甲同学至少有4次投中的概率;
(2)求乙同学投篮次数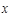 的分布列和数学期望.
的分布列和数学期望.
选修4—4:不等式选讲
已知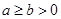 ,求证:
,求证: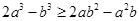 .
.
(本小题满分10分)选修4—3:坐标系与参数方程
已知直线l经过点P( ,1),倾斜角α=
,1),倾斜角α=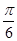 ,圆C的极坐标方程为
,圆C的极坐标方程为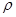 =
=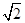 cos(θ-
cos(θ-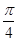 ).
).
(Ⅰ)写出直线l的参数方程,并把圆C的方程化为直角坐标方程;
(Ⅱ)设l与圆C相交于A,B两点,求点P到A,B两点的距离之积.
(本小题满分10分,选修4—2:矩阵与变换)
已知矩阵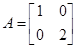 ,
,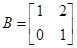 ,若矩阵
,若矩阵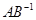 对应的变换把直线
对应的变换把直线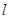 变为直线
变为直线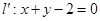 ,求直线
,求直线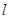 的方程.
的方程.