（本小题满分10分）选修4—3：坐标系与参数方程
已知直线l经过点P（
，1），倾斜角α＝
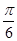，圆C的极坐标方程为
＝
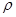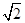cos（θ－
）．
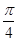（Ⅰ）写出直线l的参数方程，并把圆C的方程化为直角坐标方程；
（Ⅱ）设l与圆C相交于A，B两点，求点P到A，B两点的距离之积．
（本小题满
分15分）
已
知椭圆
的离心率
，过点
和
的直线与原点的距离为
.
（1）求椭圆的方程；
（2）设
为椭圆的左、右焦点，过
作直线交椭圆于
、
两点，求
的内切圆半径
的最大值.
（本小题满分14分）
如图（1）已知矩形
中，
，
、
分别是
、
的中点，点
在
上，且
，把
沿着
翻折，使点
在平面
上的射影恰为点（如图（2））。
（1）求证：平面
平面
；
（2）求二面角
的大小.
图（1）图（2）
（本小题满分14分）
桌面上有三颗均匀的骰子（6个面上分别标有数字1，2，3，4，5，6）。重复下面的操作，直到桌
面上没有骰子：将骰子全部抛掷，然后去掉那些朝上点数为奇数的骰子。记操作三次之内（含三次）去掉的骰子的颗数为X.
（1）求
；
（2）求X的分布列及期望
.
（本小题
满分14分）
已知
的三个内角
、
、
所对的边分别为
,向量
，且
.
（1）求角A的大小；
（2）若
，试判断
取得最大值时形状.
（本小题满分12分）
已知A、B、C是直线l上的三点，O是直线l外一点，向量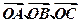
满足
＝[f(x
)＋2f′(1)]
－ln(x＋1)
。
（Ⅰ）求函数y＝f(x)的表达式； （Ⅱ）若x>0，证明：f(x)> 
；
（Ⅲ）若不等式
x2≤f(x2)＋m2－2m－3对x∈[－1,1]恒成立，求实数m的取值范围。