（本小题满分12分）
已知A、B、C是直线l上的三点，O是直线l外一点，向量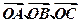
满足
＝[f(x
)＋2f′(1)]
－ln(x＋1)
。
（Ⅰ）求函数y＝f(x)的表达式； （Ⅱ）若x>0，证明：f(x)> 
；
（Ⅲ）若不等式
x2≤f(x2)＋m2－2m－3对x∈[－1,1]恒成立，求实数m的取值范围。
已知定点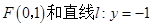
，过点F且与直线
相切的动圆圆心为点M，记点M的轨迹为曲线E.
（1）求曲线E的方程；
（2）若点A的坐标为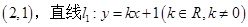
，与曲线E相交于B，C两点，直线AB，AC分别交直线于点S，T.试判断以线段ST为直径的圆是否恒过两个定点？若是，求这两个定点的坐标；若不是，说明理由.
已知函数
为自然对数的底数）．
（1）求曲线
在
处的切线方程；
（2）若
是
的一个极值点，且点
，
满足条件：
.
（ⅰ）求的值；
（ⅱ）求证：点
，
，
是三个不同的点，且构成直角三角形．
设向量
，定义一种向量积
．
已知向量
，
，点
为
的图象上的动点，点
为
的图象上的动点，且满足
（其中
为坐标原点）．
（1）请用
表示
；
（2）求的表达式并求它的周期；
（3）把函数图象上各点的横坐标缩小为原来的
倍（纵坐标不变），得到函数
的图象.设函数
，试讨论函数
在区间
内的零点个数.
（已知抛物线
（
）的准线与
轴交于点
．
（1）求抛物线的方程，并写出焦点坐标；
（2）是否存在过焦点的直线
（直线与抛物线交于点
，
），使得三角形
的面积
？若存在，请求出直线的方程；若不存在，请说明理由．
如图，在三棱锥
中，平面
平面
，
于点
，且
，
，
（1）求证：
（2）
（3）若
，
，求三棱锥的体积．