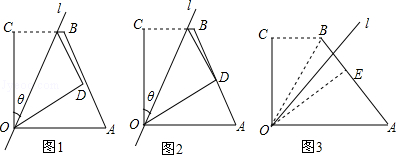
如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.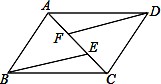
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.
在3×3的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在备用图中画出4个这样的△DEF(不能重复).
已知5a+2的立方根是3,3a+b-1的算术平方根是4,c是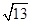 的整数部分,
的整数部分,
求3a-b+c的平方根.
问题解决
(1)如图(1),将正方形纸片ABCD折叠,使点B落在CD边上一点E(不与点C,D重合),压平后得到折痕MN.当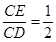 时,求
时,求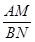 的值.
的值.
类比归纳
(2)在图(1)中,若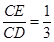 则
则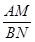 的值等于;若
的值等于;若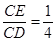 则
则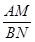 的值等于;若
的值等于;若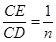 (
(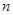 为整数),则
为整数),则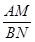 的值等于.(用含
的值等于.(用含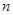 的式子表示)
的式子表示)
联系拓广
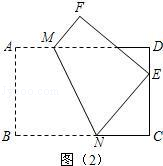
(3)如图(2),将矩形纸片ABCD折叠,使点B落在CD边上一点E(不与点C,D重合),压平后得到折痕MN,设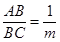 (
(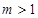 ),
),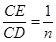 ,则
,则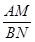 的值等于.
的值等于.
(用含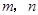 的式子表示)
的式子表示)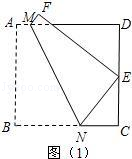
如图1,四边形OABC中,OA=a,OC=3,BC=2,∠AOC=∠BCO=90°,经过点O的直线l将四边形分成两部分,直线l与OC所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处(如图1).
(1)若折叠后点D恰为AB的中点(如图2),求θ的度数;
(2)若θ=45°,四边形OABC的直角∠OCB沿直线l折叠后,
①点B落在点四边形OABC的边AB上的E处(如图3),求a的值;
②若点E落在四边形OABC的外部,直接写出a的取值范围.