如图，△ABC中,∠C=Rt∠，AB=5cm，BC=3cm，若动点P从点C开始，按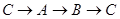
的路径运动，且速度为每秒1㎝，设出发的时间为t秒.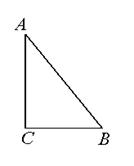
(1)出发2秒后，求△ABP的周长.
(2)问t为何值时，△BCP为等腰三角形？
(3)另有一点Q，从点C开始，按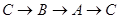
的路径运动，且速度为每秒2㎝，若P、Q两点同时出发，当P、Q中有一点到达终点时，另一点也停止运动。当t为何值时，直线PQ把△ABC的周长分成相等的两部分？(其中(3)直接写出答案即可)
如图，△ABC中，DE∥BC，EF∥AB.证明：△ADE∽△EFC．
解方程：
如图，将一副三角板，如图放置在桌面上，让三角板OAB的30°角顶点与三角板OCD的直角顶点重合，边OA与OC重合，固定三角板OCD不动，把三角板OAB绕着顶点O顺时针转动，直到边OB落在桌面上为止。
（1）如下图，当三角板OAB转动了20°时，求∠BOD的度数；
（2）在转动过程中，若∠BOD=20°，在下面两图中分别画出∠AOB的位置，并求出转动了多少度？
（3）在转动过程中，∠AOC与∠BOD有怎样的等量关系，请你给出相等关系式，并说明理由；
一个三位数，十位上的数字是百位上数字的2倍，十位上的数字比个位上的数字大1.
（1）若设百位上的数字为a，则个位数字为，这个三位数可表示为；
（2）这个三位数能被5整除吗？若能，求出这个三位数；若不能请说明理由.
某考察队从营地P处出发，沿北偏东60°前进了3km到达A地，再向正南方向前进3km最后达C地．回答下列问题：
（1）用1cm代表1千米，画出考察队行进路线图；
（2）度量出C地在营地的什么方向上？（精确到1°）
（3）测算出考察队此时离营地实际多远？（精确到0.1千米）