如图，在平面直角坐标系xOy中，直线AB与x轴交于点A，与y轴交于点B，且OA = 3，AB = 5．点P从点O出发沿OA以每秒1个单位长的速度向点A匀速运动，到达点A后立刻以原来的速度沿AO返回；点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动．伴随着P、Q的运动，DE保持垂直平分PQ，且交PQ于点D，交折线QB－BO－OP于点E．点P、Q同时出发，当点Q到达点B时停止运动，点P也随之停止．设点P、Q运动的时间是t秒（t＞0）．
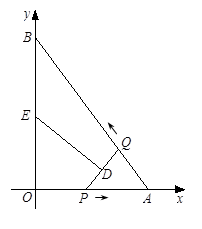
（1）求直线AB的解析式；
（2）在点P从O向A运动的过程中，求△APQ的面积S与t之间的函数关系式（不必写出t的取值范围）；
（3）在点E从B向O运动的过程中，完成下面问题：
①四边形QBED能否成为直角梯形？若能，请求出t的值；若不能，请说明理由；
②当DE经过点O时，请你直接写出t的值．
某学校准备成立男女校足球队，为了解全校学生对足球的喜爱程度，该校设计了一个调查问卷，将喜爱程度分为A（非常喜欢）、B（喜欢）、C（不太喜欢），D（很不喜欢）四种类型，并派学生会会员进行市场调查，其中一名学生会会员小丽在校门口对上学学生进行了随机调查，并根据调查结果制成了如下两幅不完整的统计图，请结合统计图所给信息解答下列问题：
（1）在扇形统计图中C所占的百分比是；小丽本次抽样调查的人数共有人；请将折线统计图补充完整；
（2）为了解少数学生很不喜欢足球的原因，小丽决定在上述调查结果中从“很不喜欢”足球的学生里随机选出两位进行回访，请你用列表法或画树状图的方法，求所选出的两位学生恰好是一男一女的概率．
如图所示，A．B两地之间有一条河，原来从A地到B地需要经过桥DC，沿折线A→D→C→B到达，现在新建了桥EF，可直接沿直线AB从A地到达B地．已知BC＝12km，∠A＝45°，∠B＝37°．桥DC和AB平行且等长，则现在从A地到达B地可比原来少走多少路程？（结果精确到0.1km．参考数据：
≈l．41，sin37°≈0.60，cos37°≈0.80）
如图，△ACB与△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°，点D为AB边上的一点，
（1）求证：△ACE≌△BCD；
（2）若DE＝13，BD＝12，求线段AB的长．
解方程：
先化简，再求值：
，其中x是方程
的根．