勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,利用面积法进行证明,著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.
[定理表述]
请你根据图1中的直角三角形,写出勾股定理内容;
[尝试证明]
以图1中的直角三角形为基础,可以构造出以a、b为底,以a+b为高的直角梯形(如图2),请你利用图2,验证勾股定理.
(内江)如图,抛物线与x轴交于点A( ,0)、点B(2,0),与y轴交于点C(0,1),连接BC.
,0)、点B(2,0),与y轴交于点C(0,1),连接BC.
(1)求抛物线的函数关系式;
(2)点N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t(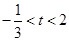 ),求△ABN的面积S与t的函数关系式;
),求△ABN的面积S与t的函数关系式;
(3)若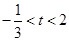 且
且 时△OPN∽△COB,求点N的坐标.
时△OPN∽△COB,求点N的坐标.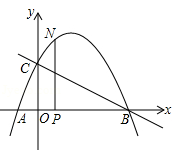
(南充)已知抛物线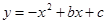 与x轴交于点A(m﹣2,0)和B(2m+1,0)(点A在点B的左侧),与y轴相交于点C,顶点为P,对称轴为l:x=1.
与x轴交于点A(m﹣2,0)和B(2m+1,0)(点A在点B的左侧),与y轴相交于点C,顶点为P,对称轴为l:x=1.
(1)求抛物线解析式.
(2)直线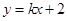 (
(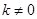 )与抛物线相交于两点M(
)与抛物线相交于两点M(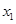 ,
,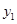 ),N(
),N(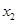 ,
,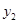 )(
)(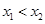 ),当
),当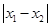 最小时,求抛物线与直线的交点M与N的坐标.
最小时,求抛物线与直线的交点M与N的坐标.
(3)首尾顺次连接点O、B、P、C构成多边形的周长为L,若线段OB在x轴上移动,求L最小值时点O,B移动后的坐标及L的最小值.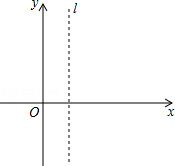
如图,△ABC为等边三角形,以边BC为直径的半圆与边AB,AC分别交于D,F两点,过点D作DE⊥AC,垂足为点E.
(1)判断DF与⊙O的位置关系,并证明你的结论;
(2)过点F作FH⊥BC,垂足为点H,若AB=4,求FH的长(结果保留根号).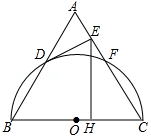
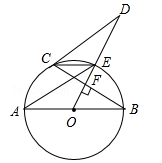
(攀枝花)如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有点E,且EF=ED.
(1)求证:DE是⊙O的切线;
(2)若OF:OB=1:3,⊙O的半径R=3,求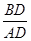 的值.
的值.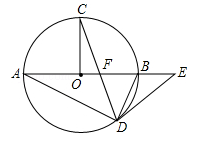
(巴中)如图,AB是⊙O的直径,OD⊥弦BC于点F,交⊙O于点E,连结CE、AE、CD,若∠AEC=∠ODC.
(1)求证:直线CD为⊙O的切线;
(2)若AB=5,BC=4,求线段CD的长.