如图,四边形ABCD,已知∠A=90°,AB=3,BC=12,CD=13,DA=4.求四边形的面积.
如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AECF是正方形?
如图,正方形ABCD绕点A逆时针旋转no后得到正方形AEFG,EF与CD交于点O.
(1)以图中已标有字母的点为端点连结两条线段(正方形的对角线除外),要求所连结的两条线段相交且互相垂直,并说明这两条线段互相垂直的理由;
(2)若正方形的边长为2cm,重叠部分(四边形AEOD)的面积为 cm2,求旋转的角度n.
cm2,求旋转的角度n.
如图,在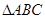 和
和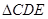 中,
中,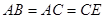 ,
,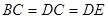 ,
,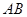 >
>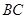 ,
,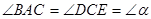 ,点
,点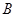 、
、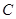 、
、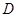 在直线
在直线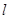 上,
上,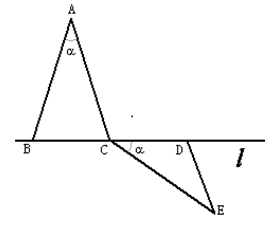
(1)按下列要求画图(保留画图痕迹):
①画出点 关于直线
关于直线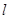 的对称点
的对称点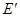 ,连接
,连接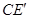 、
、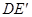 ;
;
②以点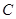 为旋转中心,将(1)中所得
为旋转中心,将(1)中所得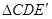 按逆时针方向旋转,使得
按逆时针方向旋转,使得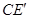 旋转后的线段
旋转后的线段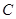
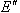 与
与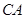 重合,得到
重合,得到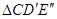 (A),画出
(A),画出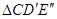 .
.
(2)解决下面问题:
①线段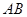 和线段
和线段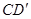 的位置关系是.并说明理由.
的位置关系是.并说明理由.
②求∠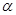 的度数.
的度数.
如图,在四边形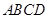 中,E、F、G、H分别是
中,E、F、G、H分别是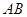 、
、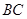 、
、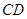 、
、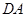 的中点.
的中点.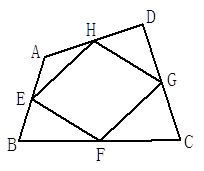
(1)请判断四边形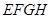 的形状.并说明为什么?
的形状.并说明为什么?
(2)若使四边形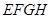 为正方形,那么四边形
为正方形,那么四边形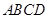 的对角线应具有怎样的性质?
的对角线应具有怎样的性质?
在梯形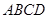 中,
中,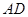 ∥
∥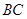 ,
,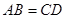 ,
,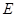 为
为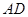 中点.
中点.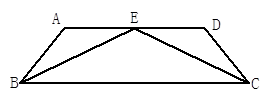
(1)求证: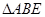 ≌
≌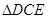 .(2)若
.(2)若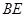 平分
平分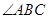 ,且
,且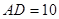 ,求
,求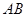 的长.
的长.