为了估计养鱼池里有多少条鱼,养鱼者,然后放回池中,经过一段时间,待带标记的鱼完全混合于鱼群后,再捕第二次样品鱼120条,其中带标记的鱼有15条,试估计鱼池中约有鱼多少条?
钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设M,N为该岛的东西两端点)最近距离为12海里(即MC=12海里).在A点测得岛屿的西端点M在点A的东北方向;航行4海里后到达B点,测得岛屿的东端点N在点B的北偏东60°方向,(其中N,M,C在同一条直线上如图),求钓鱼岛东西两端点MN之间的距离. 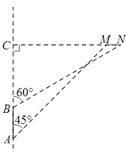
小刚很擅长球类运动,课外活动时,足球队、篮球队都力邀他到自己的阵营,小刚左右为难,最后决定通过掷硬币来确定。游戏规则如下:连续抛掷硬币三次,如果三次正面朝上或三次反面朝上,则由小刚任意挑选两球队;如果两次正面朝上一次正面朝下,则小刚加入足球阵营;如果两次反面朝上一次反面朝下,则小刚加入篮球阵营。
(1)用画树状图的方法表示三次抛掷硬币的所有结果。
(2)小刚任意挑选两球队的概率有多大?
(3)这个游戏规则对两个球队是否公平?为什么?
先化简,再求值: ,其中
,其中
如图,抛物线 交
交 轴于A、B两点,交
轴于A、B两点,交 轴于点C,
轴于点C,
点P是它的顶点,点A的横坐标是 3,点B的横坐标是1.
3,点B的横坐标是1.
(1)求 、
、 的值;
的值;
(2)求直线PC的解析式;
(3)请探究以点A为圆心、直径为5的圆与直线PC的位置关系,并说明理由.
(参考数据 ,
, ,
, )
)
已知⊙O中,AC为直径,MA、MB分别切⊙O于点A、B.
(1)如图①,若∠BAC=25°,求∠AMB的大小;
(2)如图②,过点B作BD⊥AC于E,交⊙O于点D,若BD=MA,求∠AMB的大小.