如图是多用表的刻度盘,当选用量程为50mA的电流档测量电流时,表针指于图示位置,则所测电流为_____mA;若选用倍率为“×100”的电阻档测电阻时,表针也指示在图示同一位置,则所测电阻的阻值为______Ω,如果要用此多用表测量一个约2.0×104Ω的电阻,为了使测量比较精确,应选的欧姆档是________(选填“×10”、“×100”或“×1K”),换档结束后,实验操作上首先要进行的步骤是____ .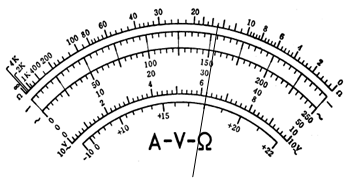
某同学做“验证力的平行四边形定则”实验时,主要步骤是:
| A.在桌上放一块方木板,在方木板上铺一张白纸,用图钉把白纸钉在方木板上 |
| B.用图钉把橡皮条的一端固定在板上的A点,在橡皮条的另一端拴上两条细绳,细绳的另一端系着绳套 |
| C.用两个弹簧秤分别钩住绳套,互成角度地拉橡皮条,使橡皮条伸长,结点到达某一位置O.记录下O点的位置,读出两个弹簧秤的示数 |
| D.按选好的标度,用铅笔和刻度尺作出两只弹 |
簧秤的拉力F1和F2的图示,并用平行四边形定则求出合力F
E. 只用一只弹簧秤,通过细绳套拉橡皮条使其伸长,读出弹簧秤的示数,记下细绳的方向,按同一标度作出这个力F′的图示.
F. 比较力F′和F的大小和方向,看它们是否相同,得出结论.
上述步骤中:
①有重要遗漏的步骤的序号是和;
②遗漏的内容分别是和
有一个小灯泡上标有“3.8V、0.5A”的字样,现要描绘这个灯泡的伏安特性曲线。有下列器材供选用:
A.电压表(0~5 V,内阻约为10 kΩ)
B.电流表(0~0.6A,内阻约为0.5Ω)
C.电流表(0~3A,内阻约为0.1Ω)
D.滑动变阻器(0~10Ω,2A)
E.滑动变阻器(0~1kΩ,0.1 A)
F.学生电源(直流6V),还有开关、导线若干
①实验中所用电流表应选用,滑动变阻器应选用。
②实验时要求尽量减少实验误差,测量电压从零开始多取几组数据,应选用图甲中图所示电路进行实验。
③某同学根据实验得到的数据画出了该小灯泡的伏安特性曲线(如图乙所示),若用电动势为3.2V、内阻为3Ω的电源给该小灯泡供电,则该小灯泡的实际功率是W。
某同学用如图所示电路来测定电池的电动势和内阻。
①实验开始时,滑片P应位于_________端。(填A或B)
②该同学测得如下表的五组数据。根据数据在答题卷相应图中作出U-I图线,从图象可得电池的电动势E=________V,内阻r=___________Ω。(结果均保留二位小数)。

 |
1 |
2 |
3 |
4 |
5 |
| U/V |
1.37 |
1.32 |
1.24 |
1.10 |
1.05 |
| I/A |
0.12 |
0.20 |
0.31 |
0.50 |
0.57 |
某同学设计了如图所示的电路测电源电动势E及电阻R1的阻值。实验器材有:待测电源E,待测电阻R1,定值电阻R2,电流表A(量程为0.6A,内阻不计),电阻箱R(0-99.99Ω),单刀单掷开关S1,单刀双掷开关S2,导线若干。
(1)先测电阻R1的阻值(R1只有几欧姆)。请将小明同学的操作补充完整:闭合S1,将S2切换到a,调节电阻箱,读出其示数r1和对应的电流表示数l,将S2切换到b,,读出此时电阻箱的示数r2,则电阻R1的表达式为R1=。
(2)该同学已经测得电阻R1=2.Ω,继续测电源电动势E。该同学的做法是:闭合S1,将S2切换到b,多次调节电阻箱.读出多组电阻箱示数R和对应的电流表示数I,由测得的数据,绘出了如图中所示的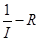 图线.则电源电动势E=V:
图线.则电源电动势E=V:
如图所示是小徐同学做“探究做功与速度变化的关系”的实验装置。他将光电门固定在直轨道上的O点,用同一重物通过细线拉同一小车,每次小车都从不同位置由静止释放,各位置A、B、C、D、E、F、G(图中只标出了O、G)离O点的距离d分别为8cm、16cm、24cm、32cm、40cm、48cm,56cm。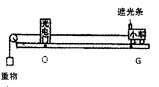
(1)该实验是否需要测量重物的重力(填“需要”或“不需要”);
(2)该实验是否必须平衡摩擦力?(填“是”或“否”);
(3)为了探究做功与速度变化的规律,依次得到的实验数据记录如下表所示。请选取其中最合适的两行数据在答题卷的方格纸内描点作图。
(4)从图像得到的直接结论是,从而间接得到做功与物体速度变化的规律是。