设函数f(x)在R上可导,其导函数为f/(x),且函数y=(1−x) f/(x)的图像如图所示,则下列结论中一定成立的是
| A.函数f(x)有极大值f(2)和极小值f(1) |
| B.函数f(x)有极大值f(−2)和极小值f(1) |
| C.函数f(x)有极大值f(2)和极小值f(−2) |
| D.函数f(x)有极大值f(−2)和极小值f(2) |
若实数a、b满足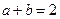 ,则
,则 的最小值是 ()
的最小值是 ()
| A.18 | B.6 | C.2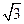 |
D.2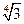 |
记等差数列的前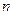 项和为
项和为 ,若
,若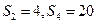 ,则该数列的公差
,则该数列的公差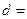 ()
()
| A.2 | B.3 | C.6 | D.7 |
函数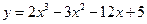 在区间
在区间 上最大值与最小值分别是()
上最大值与最小值分别是()
| A.5,-16 | B.5,-4 | C.-4,-15 | D.5,-15 |
已知函数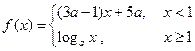 ,现给出下列命题:
,现给出下列命题:
① 当图象是一条连续不断的曲线时,则 =
=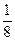 ;
;
② 当图象是一条连续不断的曲线时,能找到一个非零实数 ,使得f (x)在R上是增函数;
,使得f (x)在R上是增函数;
③ 当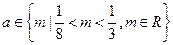 时,不等式
时,不等式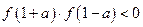 恒成立;
恒成立;
④ 函数 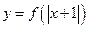 是偶函数 . 其中正确的命题是 ()
是偶函数 . 其中正确的命题是 ()
| A.①③ | B.②④ | C.①③④ | D.①②③④ |
设函数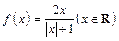 ,区间
,区间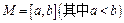 ,集合
,集合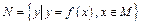 ,则使
,则使 成立的实数对
成立的实数对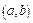 有()
有()
| A.1个 | B.3个 | C.2个 | D.0个 |