解不等式组：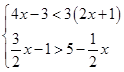
．已知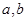
为实数，且
，求
的平方根。
如图，在
□ABCD中，
于点E，
于点F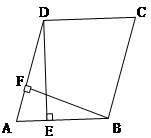
（1）说明：
（2）□ABCD周长为12，AD：DE=3：2，求DE+BF的值。
．解方程： 
分解因式（1）
(5分)
（2）
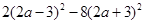(5分)
某物流公司的甲、乙两辆货车分别从相距300千米的A、B两地同时出发相向而行，并以各自的速度匀速行驶， 1.5小时时甲车先到达配货站C地，此时两车相距30千米，甲车在C地用1小时配货，然后按原速度开往B地；2小时时乙车也到达C地，乙车未停留直接开往A地．乙车的速度是千米/小时，B、C两地的距离是千米，A、C两地的距离是千米；
（2）求甲车的速度及甲车到达B地所用的时间；
（3）乙车出发多长时间，两车相距150千米？