如图所示,已知空间四边形ABCD,E、F分别是边AB、AD的中点,F、G分别是边BC、CD上的点,且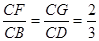 ,求证直线EF、GH、AC交于一点.
,求证直线EF、GH、AC交于一点.
2015年某市某区高考文科数学成绩抽样统计如下表:
(1)求出表中m、n、M、N的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;(纵坐标保留了小数点后四位小数)
(2)若2015年某市高考文科考生共有20000人,试估计全市文科数学成绩在90分及90分以上的人数;
(3)香港某大学对内地进行自主招生,在参加面试的学生中,有7名学生数学成绩在140分以上,其中男生有4名,要从7名学生中录取2名学生,求其中恰有1名女生被录取的概率.
如图,已知四边形 与
与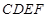 均为正方形,平面
均为正方形,平面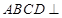 平面
平面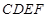 .
.
(1)求证: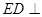 平面
平面 ;
;
(2)求二面角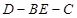 的大小.
的大小.
已知椭圆 :
: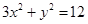 ,直线
,直线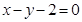 交椭圆
交椭圆 于
于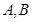 两点.
两点.
(Ⅰ)求椭圆 的焦点坐标及长轴长;
的焦点坐标及长轴长;
(Ⅱ)求以线段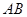 为直径的圆的方程.
为直径的圆的方程.
在打靶训练中,某战士射击一次的成绩在9环(包括9环)以上的概率是0.18,在8~9环(包括8环)的概率是0.51,在7~8环(包括7环)的概率是0.15,在6~7环(包括6环)的概率是0.09.计算该战士在打靶训练中射击一次取得8环(包括8环)以上成绩的概率和该战士打靶及格(及格指6环以上包括6环)的概率.
已知 为椭圆
为椭圆 上的三个点,
上的三个点, 为坐标原点.
为坐标原点.
(1)若 所在的直线方程为
所在的直线方程为 ,求
,求 的长;
的长;
(2)设 为线段
为线段 上一点,且
上一点,且 ,当
,当 中点恰为点
中点恰为点 时,判断
时,判断 的面积是否为常数,并说明理由.
的面积是否为常数,并说明理由.