若复数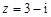
，则
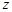在复平面内对应的点位于（）
| A．第一象限 | B．第二象限 |
| C．第三象限 | D．第四象限 |
函数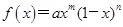
在区间[0,1]上的图象如图所示，则m，n的值可能是（ ）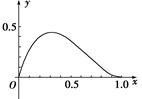
| A．m＝1，n＝1 | B．m＝1，n＝2 |
| C．m＝2，n＝1 | D．m＝3，n＝1 |
设f（x）、g（x）分别是定义在R上的奇函数和偶函数，g（x）恒不为0，当x＜0时，f（x）g（x）－f（x）g′（x）＞0，且f（3）＝0，则不等式f（x）g（x）＜0的解集是（ ）
| A．（－3,0）∪（3，＋∞） |
| B．（－3,0）∪（0,3） |
| C．（－∞，－3）∪（3，＋∞） |
| D．（－∞，－3）∪（0,3） |
炼油厂某分厂将原油精炼为汽油，需对原油进行冷却和加热，如果第x小时，原油温度（单位：℃）为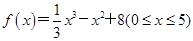
，那么，原油温度的瞬时变化率的最小值是（ ）
| A．8 | B． |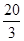
C．－1 | D．－8 |
观察下列各式：
，…，则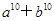
＝（ ）
| A．28 | B．76 | C．123 | D．199 |
，则
（ ）
