先化简代数式 ,然后取你喜欢的一组
,然后取你喜欢的一组 的值代入求值(提示:所取的值必须使代数式有意义)
的值代入求值(提示:所取的值必须使代数式有意义)
某校为了解该校九年级学生2016年适应性考试数学成绩,现从九年级学生中随机抽取部分学生的适应性考试数学成绩,按 , , , 四个等级进行统计,并将统计结果绘制成如图所示不完整的统计图,请根据统计图中的信息解答下列问题:
(说明: 等级:135分 分 等级:120分 分, 等级:90分 分, 等级:0分 分)
(1)此次抽查的学生人数为 ;
(2)把条形统计图和扇形统计图补充完整;
(3)若该校九年级有学生1200人,请估计在这次适应性考试中数学成绩达到120分(包含120分)以上的学生人数.

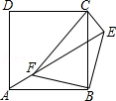
如图,点 正方形 外一点,点 是线段 上一点, 是等腰直角三角形,其中 ,连接 、 .
(1)求证: ;
(2)判断 的形状,并说明理由.
教室里有4排日光灯,每排灯各由一个开关控制,但灯的排数序号与开关序号不一定对应,其中控制第二排灯的开关已坏(闭合开关时灯也不亮).
(1)将4个开关都闭合时,教室里所有灯都亮起的概率是 ;
(2)在4个开关都闭合的情况下,不知情的雷老师准备做光学实验,由于灯光太强,他需要关掉部分灯,于是随机将4个开关中的2个断开,请用列表或画树状图的方法,求恰好关掉第一排与第三排灯的概率.
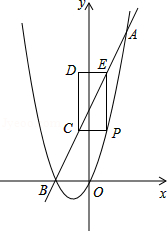
如图,已知抛物线 与直线 交于 、 两点,点 是抛物线上 、 之间的一个动点,过点 分别作 轴、 轴的平行线与直线 交于点 和点 .
(1)求抛物线的解析式;
(2)若 为 中点,求 的长;
(3)如图,以 , 为边构造矩形 ,设点 的坐标为 ,请求出 , 之间的关系式.
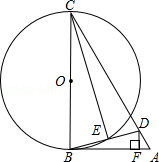
如图,在 中, 为 上一点,且 ,以 为直径作 ,交 于点 ,连接 ,过 作 于点 , .
(1)求证: 是 的切线;
(2)若 , ,求 的直径 的长.