如图,等腰梯形ABCD中,AD∥BC,AB=DC,AC⊥BD,过D点作DE∥AC交BC的延长线于E点.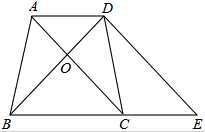
(1)求证:四边形ACED是平行四边形;
(2)求证:三角形BDE是等腰直角三角形。
(8)如图,在宽为20米、长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米2,则修建的路宽应为多少米?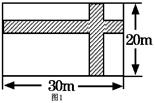
解方程(16)
(1)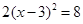 (直接开平方法)
(直接开平方法)
(2)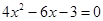 (配方法)
(配方法)
(3)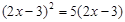 (分解因式法)
(分解因式法)
(4)(x+8)(x+1)=-12(运用适当的方法)
如图,矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q。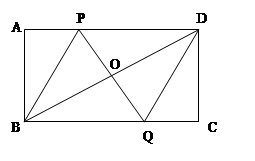
(1)求证:OP=OQ;
(2)若AD=8厘米,AB=6厘米,P从点A出发,以1厘米/秒的速度向D运动(不与D重合)。设点P运动时间为t秒,请用t表示PD的长;并求t为何值时,四边形PBQD是菱形。
一块长方形草地的长和宽分别为20m和15m,在它四周外围环绕着宽度相等的小路,已知小路的面积为246㎡,求小路的宽度。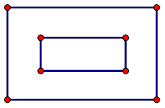
两个数的差是2,积是15,求这两个数。