(1)如图所示,用5个小正方体搭成的立体图形,请你从正面、左面、上面观察这个几何体,分别画出你所看到的几何体的形状图;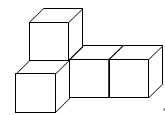
(2)一个几何体由几块大小相同的小立方体搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置小立方块的个数,请画出这个几何体从正面、左面观察的形状图.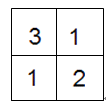
在求1+2+22+23+24+25+26的值时,小明发现:从第二个加数起每一个加数都是前一个加数的2倍,于是他设:S=1+2+22+23+24+25+26①然后在①式的两边都乘以2,得:2S=2+22+23+24+25+26+27 ②;②﹣①得2S﹣S=27﹣1,S=27﹣1,即1+2+22+23+24+25+26=27﹣1.
(1)求1+3+32+33+34+35+36的值;
(2)求1+a+a2+a3+…+a2013(a≠0且a≠1)的值.
(1)解不等式: ;
;
(2)求不等式组 的整数解.
的整数解.
(1)计算:(﹣a)7÷(﹣a)4×(﹣a)3;
(2)利用乘法公式计算:2014×2016﹣20152;
(3)因式分解:x3﹣4x.
如图,已知直线y=2x分别与双曲线y= ,y=
,y= (x>0)交于P、Q两点,且OP=2OQ,点A是双曲线y=
(x>0)交于P、Q两点,且OP=2OQ,点A是双曲线y= 上的动点,过A作AB∥x轴,AC∥y轴,分别交双曲线y=
上的动点,过A作AB∥x轴,AC∥y轴,分别交双曲线y= (x>0)于点B、C.连接BC.
(x>0)于点B、C.连接BC.
(1)求k的值;
(2)随着点A的运动,△ABC的面积是否发生变化?若不变,求出△ABC的面积,若改变,请说明理由.
(3)直线y=2x上是否存在点D,使得点A、B、C、D为顶点的四边平行四边形?若能,求出相应点A的坐标;若不能,请说明理由.
一辆汽车开往距离出发地180千米的目的地,出发后第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前40分到达目的地.求前一小时的行驶速度.