解答发现：⑴ 当a＝3，b＝2时，分别求代数式（a＋b）2和a2＋2ab＋b2的值，并观察这两个代数式的值有什么关系？
⑵再多找几组你喜欢的数试一试，从中你发现了什么规律？
⑶利用你所发现的规律计算a＝1. 625，b＝0. 375时，a2＋2ab＋b2的值？
（本小题共6分）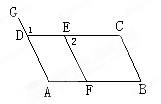
如图,点E在CD上,点F在BA上,G是AD延长线上一点. 
(1)若∠A
=∠1,则可判断_______∥_______,因为________.
(2)若∠1=∠_______,则可判断AG∥BC，因为_________.
(3)若∠2+∠_______=180°,则可判断CD∥AB,因为______
______.
（本小题共5分）已知，线段AB=80cm,M为线段AB的中点，点P在线段MB上，N为线段PB的中点，且NB="14" cm,求线段MP的长。
（本小题共5分）一家三口在假期期间去北方旅游，当地有甲、乙两家旅游社，其定价一样，但对家庭旅游都有优惠，甲旅行社表示大人不打折，小孩打六折；乙旅行社表示一家三口全都打八折，经核算，乙旅行社要便宜240元，问成人定价多少元？
（1）先化简，再求值：3（2m2-n+4）-2（-m2+3n-1）,其中m=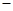
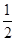,n=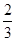
（2）已知多项式A=3x2-5xy,B=3xy-x2,C=8x2-5xy,求2A-5B+3C
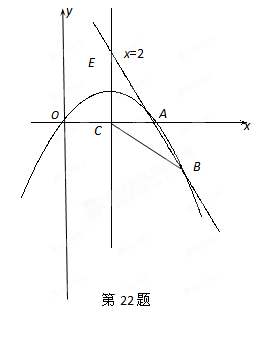
如图，已知抛物线经过原点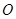
和
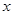轴上另一点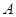
，它的对称轴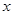="2" 与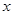轴交于点
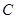，直线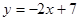
经过抛物线上一点
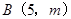，且与直线
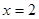交于点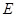
.
求
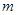的值及该抛物线的函数关系式；若点
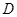是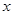轴上一动点，当△
△∽△
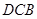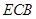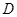时，求点的坐标；若
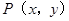是该抛物线上的一个动点，是否存在这样的点
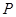,使得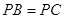
,若存在，试求出所有符合条件的点P的坐标；若不存在，请说明理由.