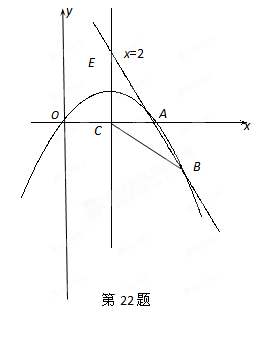
如图,已知抛物线经过原点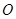 和
和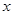 轴上另一点
轴上另一点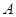 ,它的对称轴
,它的对称轴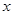 ="2" 与
="2" 与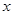 轴交于点
轴交于点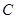 ,直线
,直线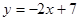 经过抛物线上一点
经过抛物线上一点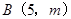 ,且与直线
,且与直线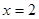 交于点
交于点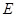 .
.
求
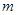 的值及该抛物线的函数关系式;
的值及该抛物线的函数关系式;若点
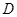 是
是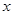 轴上一动点,当△
轴上一动点,当△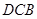 △∽△
△∽△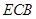 时,求点
时,求点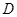 的坐标;
的坐标;若
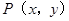 是该抛物线上的一个动点,是否存在这样的点
是该抛物线上的一个动点,是否存在这样的点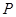 ,使得
,使得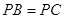 ,若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由.
,若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由.
如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转900,得到△DOC。抛物线y=ax2+bx+c经过点A、B、C。
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t。
①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F。求出当△CEF与△COD相似时点P的坐标;
②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD面积的最大值;若不存在,请说明理由。
如图,已知A(﹣4, ),B(﹣1,2)是一次函数y=kx+b与反比例函数y=
),B(﹣1,2)是一次函数y=kx+b与反比例函数y= (m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,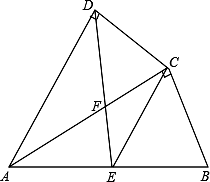
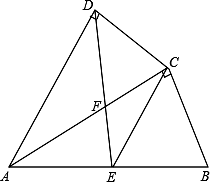
(1)求证:AC2=AB•AD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求 的值.
的值.
如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度(结果精确到0.1m).(参考数据: ≈1.414,
≈1.414, ≈1.732)
≈1.732)
已知如图所示,AB为⊙O的直径,C、D是半圆弧上的两点,E是AB上除0外的一点,AC与DE相交于点F.① =
= .②DE
.②DE AB,③AF=DF.
AB,③AF=DF.
(1)写出以“①②③中的任意两个为条件,推出第三个(结论)”的一个正确命题,并加以证明;
(2)以“①②③中的任意两个为条件,推出第三个(结论)”可以组成多少个正确的命题?(1)中的除外,不必说明理由)