如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转900,得到△DOC。抛物线y=ax2+bx+c经过点A、B、C。
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t。
①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F。求出当△CEF与△COD相似时点P的坐标;
②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD面积的最大值;若不存在,请说明理由。
.(本题15分)
马田同学将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙相切,她把切点记为A、B,然后,她又在桌子边缘上任取一点P(异于A、B),通过计算∠APB的度数,她惊奇的发现∠APB的度数的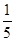 ,正好都和她今天作业中的一条抛物线与x轴的交点的横坐标完全相同,她作业中的那条抛物线还经过点C(10,17).聪明的你:
,正好都和她今天作业中的一条抛物线与x轴的交点的横坐标完全相同,她作业中的那条抛物线还经过点C(10,17).聪明的你: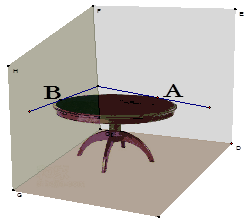 (1)请你求出∠APB的度数
(1)请你求出∠APB的度数
(2)请你求出马田同学作业中的
那条抛物线的对称轴方程.
(本题12分)
某饰品店店老板去批发市场购买新款手链,第一次购手链共用100元,按该手链的定价2.8元现售,并很快售完.由于该手链深得年轻人喜爱十分畅销,第二次去购手链时,每条的批发价已比第一次高0.5元,共用去了150元,所购数量比第一次多10条.当这批手链售出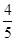 时,出现滞销,便以定价的5折售完剩余的手链,试问该老板第二次售手链是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?,若赚钱,赚多少?
时,出现滞销,便以定价的5折售完剩余的手链,试问该老板第二次售手链是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?,若赚钱,赚多少?
(本题12分)
一天晚上,身高1.6米的张雅婷发现:当她离路灯底脚(B)12米时,自己的影长(CD)刚好为3米,当她继续背离路灯的方向再前进2米(到达点F)时,她说自己的影长是(FH)5米。你认为张雅婷说的对吗?若她说的对,请你说明理由;若她说的不对,请你帮她求出她的影长(FH).
解方程:
如图,已知反比例函数 和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+1,b+k)两点.
和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+1,b+k)两点.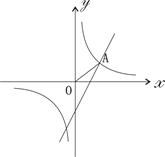
(1)求反比例函数的解析式;
(2)如下图,已知点A在第一象限,且同时在上述两个函数的图象上,求点A的坐标;
(3)利用(2)的结果,请问:在x轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由.