某化工厂生产某种化肥，每吨化肥的出厂价为1780元，其成本价为900元，但在生产过程中，平均每吨化肥有280立方米有害气体排出，为保护环境，工厂须对有害气体进行处理，现有下列两种处理方案可供选择：
①将有害气体通过管道送交废气处理厂统一处理，则每立方米需付费3元；
②若自行引进处理设备处理有害气体，则每处理1立方米有害气体需原料费0.5元，且设备每月管理、损耗等费用为28000元.设工厂每月生产化肥x吨，每月利润为y元（注：利润=总收入-总支出）
（1）分别求出用方案①、方案②处理有害气体时，y与x的函数关系式；
（2）根据工厂每月化肥产量x的值，通过计算分析工厂应如何选择处理方案才能获得最大利润.
(本题满分10分)
先化简，再求值：(3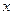
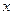+2)(3一2)一5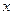(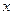一l)一(2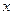一l)2，其中=－
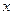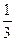
某校九年级有200名学生参加了全国初中数学联合竞赛的初赛，为了了解本次初赛的成绩情况，从中抽取了50名学生，将他们的初赛成绩(得分为整数，满分为100分)分成五组：第一组49.5～59.5；第二组59.5～69.5；第三组69.5～79.5；第四组79.5～89.5；第五组89.5～100.5．统计后得到图8所示的频数分布直方图(部分)．观察图形的信息，回答下列问题：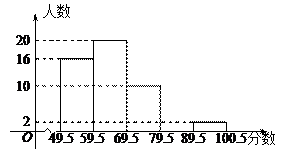
(1)第四组的频数为_____(直接写答案)．
(2)若将得分转化为等级，规定：得分低于59.5分评为“D”，59.5～69.5分评为“C”，69.5～89.5分评为“B”，89.5～100.5分评为“A”．那么这200名参加初赛的学生中，参赛成绩评为“D”的学生约有________个(直接填写答案)．
(3)若将抽取出来的50名学生中成绩落在第四、第五组的学生组成一个培训小组，再从这个培训小组中随机挑选2名学生参加决赛．用列表法或画树状图法求：挑选的2名学生的初赛成绩恰好都在90分以上的概率．
如图，东梅中学要在教学楼后面的空地上用40m长的竹篱笆围出一个矩形地块作生物园，矩形的一边用教学楼的外墙，其余三边用竹篱笆．设矩形的宽为x，面积为y．
(1)求y与x的函数关系式，并求自变量x的取值范围；
(2)生物园的面积能否达到210m2?说明理由．
(1)如图①，PA、PB分别与⊙O相切于点A、B．求证：PA＝PB．
(2)如图②，过⊙O外一点P的两条直线分别与⊙O相交于点A、B和C、D．
则当时，PB＝PD
(不添加字母符号和辅助线，不需证明，只需填上符合题意的一个条件)．
在平面直角坐标系中，点M的坐标为(a，1－2a)．
(1)当a＝－1时，点M在坐标系的第___________象限(直接填写答案)；
(2)将点M向左平移2个单位，再向上平移1个单位后得到点N，当点N在第三象限时，求a的取值范围．