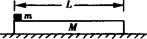
如图所示，在匀强磁场中竖直放置两条足够长的平行导轨，磁场方向与导轨所在平面垂直，磁感强度大小为B0。导轨上端连接一阻值为R的电阻和电键K，导轨电阻不计。两金属棒a和b的电阻都为R，质量分别为ma=0.02kg和mb=0.01kg，它们与导轨接触良好，并可沿导轨无摩擦地运动，g取10m/s2。
（1）若将b棒固定，电键K断开，用一竖直向上的恒力F拉a棒，稳定后a棒以v1=10m/s的速度向上匀速运动。此时再释放b棒，b棒恰能保持静止。求拉力F的大小。
（2）若将a棒固定，电键K闭合，让ｂ棒自由下滑，求b棒滑行的最大速度v2。
（3）若将a棒和b棒都固定，电键K断开，使磁感强度从B0随时间均匀增加，经0.1s后磁感强度增大到2B0时a棒所受到的安培力大小正好等于a棒的重力，求两棒间的距离h。
一弹簧的原长为10㎝，在其下端挂500N的重物时，弹簧的长度变为15㎝（此时仍在弹性范围内）；今把重物取走200N后，弹簧的伸长量应为多大？
一辆汽车从静止开始，在水平路面上以4m/s2的加速度做匀加速直线运动。 求：汽车在4s末的速度大小；
汽车在这4s内的位移大小。
两根相距为L=1m的足够长的金属导轨如图所示放置，一组导轨水平，另一组平行导轨与水平面成37°角，拐角处连接一阻值为R=1Ω的电阻。质量均为m=1kg的金属细杆ab、cd与导轨垂直接触形成闭合回路，杆与导轨之间的动摩擦因数均为μ=0.5，导轨电阻不计，两杆的电阻均为R=1Ω。整个装置处于磁感应强度大小为
B=1T，方向竖直向上的匀强磁场中。当ab杆在平行于水平导轨的拉力作用下沿导轨向右匀速运动时，静止的cd杆所受摩擦力为最大静摩擦力，方向沿斜面向下。求此拉力的功率。（重力加速度g=10m/s2. 可认为最大静摩擦力等于滑动摩擦力）
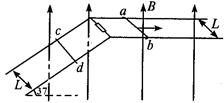
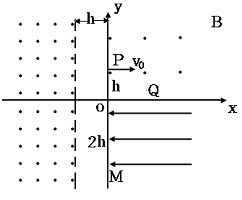
质量为m、电量为q的带电离子从P（0，h）点沿x轴正方向射入第一象限的匀强磁场中，磁感应强度为B，并沿着y轴负方向垂直进入匀强电场（电场方向沿x轴负方向），然后离子经过y轴上的M（0，－2h）点，进入宽度为h的无场区域
，如图所示，再进入另一范围足够大的匀强磁场，最后回到P点。不计重力，试求：初速度v0
电场强度E
从P点出发到再次回到P点所用的时间
如图所示，质量M="1" kg，长L="l" m的木板静止在粗糙的水平地面上，木板与地面间的动摩擦因数μ1=0．1．在木板的左端放置一个质量m=1kg，大小可以忽略的铁块，铁块与木板间的动摩擦因数μ2=0．4，认为最大静摩擦力等于滑动摩擦力，取g=10m/s2，若在铁块上加一个水平向右的恒力F="8" N，则经过多长时间铁块运动到木板的右端?