两根相距为L=1m的足够长的金属导轨如图所示放置,一组导轨水平,另一组平行导轨与水平面成37°角,拐角处连接一阻值为R=1Ω的电阻。质量均为m=1kg的金属细杆ab、cd与导轨垂直接触形成闭合回路,杆与导轨之间的动摩擦因数均为μ=0.5,导轨电阻不计,两杆的电阻均为R=1Ω。整个装置处于磁感应强度大小为 B=1T,方向竖直向上的匀强磁场中。当ab杆在平行于水平导轨的拉力作用下沿导轨向右匀速运动时,静止的cd杆所受摩擦力为最大静摩擦力,方向沿斜面向下。求此拉力的功率。(重力加速度g=10m/s2. 可认为最大静摩擦力等于滑动摩擦力)
B=1T,方向竖直向上的匀强磁场中。当ab杆在平行于水平导轨的拉力作用下沿导轨向右匀速运动时,静止的cd杆所受摩擦力为最大静摩擦力,方向沿斜面向下。求此拉力的功率。(重力加速度g=10m/s2. 可认为最大静摩擦力等于滑动摩擦力)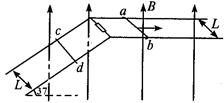
如图所示,真空中,带电荷量分别为+Q与-Q的点电荷A、B相距r,则:
(1)两点电荷连线的中点O的场强多大?
(2)在两电荷连线的中垂线上,距A、B两点都为r的O′点的场强如何?
利用油膜法可以粗略测出阿伏加德罗常数。把密度ρ=0.8×103kg/m3的某种油,用滴管滴一滴在水面上形成油膜,已知这滴油的体积为V=0.5×10-3cm3,形成的油膜面积为S=0.7m2,油的摩尔质量M=9×10-2kg/mol,若把油膜看成单分子层,每个油分子看成球形,那么:
(1)油分子的直径是多少?
(2)由以上数据可粗略测出阿伏加德罗常数NA是多少?(保留一位有效数字)
一定质量气体的体积是20L时,压强为1×105Pa。当气体的体积减小到16L时,压强为多大?设气体的温度保持不变。
如图甲所示,水平传送A、B两轮间的距离L="3.0" m,质量M="1.0" kg的物块(可视为质点)随传送带一起以恒定的速率v0向左匀速运动,当物块运动到最左端时,质量m="0.020" kg的子弹以u0="400" m/s的水平速度向右射中物块并穿出。在传送带的右端有一传感器,测出物块被击穿后的速度随时间的变化关系如图13乙所示(图中取向右运动的方向为正方向,子弹射出物块的瞬间为t=0时刻)。设子弹击穿物块的时间可忽略不计,且子弹不会击中传感器而发生危险,物块的质量不因被子弹击穿而发生改变。不计空气阻力及A、B轮的大小,取重力加速度g= 10 m/s2。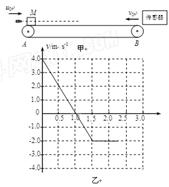
(1)求物块与传送带间的动摩擦因数m;
(2)求子弹击穿物块的过程中产生的热量Q1;
(3)如果从第一颗子弹击中物块开始,每隔Dt=1.5s就有一颗相同的子弹以同样的速度击穿物块,直至物块最终离开传送带。设所有子弹与物块间的相互作用力均相同,求整个过程中物块与传动带之间因摩擦产生的热量Q2。
雨滴在空中下落时,由于空气阻力的影响,最终会以恒定的速度匀速下降,我们把这个速度叫做收尾速度。研究表明,在无风的天气条件下,空气对下落雨滴的阻力可由公式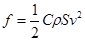 来计算,其中C为空气对雨滴的阻力系数(可视为常量),ρ为空气的密度,S为雨滴的有效横截面积(即垂直于速度v方向的横截面积)。
来计算,其中C为空气对雨滴的阻力系数(可视为常量),ρ为空气的密度,S为雨滴的有效横截面积(即垂直于速度v方向的横截面积)。
假设雨滴下落时可视为球形,且在到达地面前均已达到收尾速度。每个雨滴的质量均为m,半径均为R,雨滴下落空间范围内的空气密度为ρ0,空气对雨滴的阻力系数为C0,重力加速度为g。
(1)求雨滴在无风的天气条件下沿竖直方向下落时收尾速度的大小;
(2)若根据云层高度估测出雨滴在无风的天气条件下由静止开始竖直下落的高度为h,求每个雨滴在竖直下落过程中克服空气阻力所做的功;
(3)大量而密集的雨滴接连不断地打在地面上,就会对地面产生持续的压力。设在无风的天气条件下雨滴以收尾速度匀速竖直下落的空间,单位体积内的雨滴个数为n(数量足够多),雨滴落在地面上不反弹,雨滴撞击地面时其所受重力可忽略不计,求水平地面单位面积上受到的由于雨滴对其撞击所产生的压力大小。