在一次实践活动中,某课题学习小组用测倾器、皮尺测量旗杆的高度,他们设计了如下的方案(如图1所示):
(1)在测点A处安置测倾器,测得旗杆顶部M的仰角∠MCE=α;
(2)量出测点A到旗杆底部N的水平距离AN=m;
(3)量出测倾器的高度AC=h。
根据上述测量数据,即可求出旗杆的高度MN。
如果测量工具不变,请参照上述过程,重新设计一个方案测量某小山高度(如图2)
(1)在图2中,画出你测量小山高度MN的示意图(标上适当的字母)
(2)写出你的设计方案。 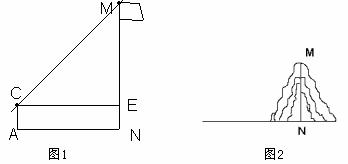
阅读材料:黑白双雄,纵横江湖;双剑合壁,天下无敌.这是武侠小说中的常见描述,其意指两个人合在一起,取长补短,威力无比.在二次根式中也有这样相辅相成的例子.
如 ,
,
它们的积是有理数,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式除法可以这样解:
如 ,
,
象这样,通过分子、分母同乘以一个式子把分母中的根号化去或根号中的分母化去,叫做分母有理化.
解决问题:
(1) 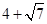 的有理化因式是.
的有理化因式是. 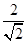 分母有理化得.
分母有理化得.
(2)分母有理化:(1) 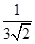 ="_________;(2)"
="_________;(2)" 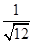 ="________;(3)"
="________;(3)"  =______..
=______..
(3)计算: 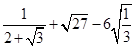 .
.
四川汶川大地震牵动了三百多万滨州人民的心,全市广大中学生纷纷伸出了援助之手,为抗震救灾踊跃捐款。滨州市振兴中学某班的学生对本校学生自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据。下图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:8:6,又知此次调查中捐款25元和30元的学生一共42人。
(1)他们一共调查了多少人?
(2)这组数据的众数、中位数各是多少?
(3)若该校共有1560名学生,估计全校学生捐款多少元?
如图,将一张矩形纸片 沿EF折叠,使点
沿EF折叠,使点 落在
落在 边上的点B处;沿BG折叠,使点
边上的点B处;沿BG折叠,使点 落在点D处,且BD过F点.
落在点D处,且BD过F点.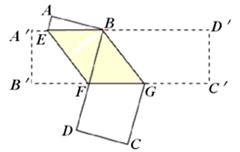
⑴试判断四边形BEFG的形状,并证明你的结论.
⑵当∠BFE为多少度时,四边形BEFG是菱形.
如图,网格中每一个小正方形的边长为1个单位长度.
⑴AB的长度为.
⑵请在所给的网格内画出以线段AB为腰、BC为下底的等腰梯形ABCD;
⑶梯形ABCD的面积等于_________.
在解方程x2+px+q=0时,小张看错了p,解得方程的根为1与-3;小王看错了q,解得方程的根为4与-2。这个方程的根应该是什么?