过山车是游乐场中常见的设施．如图17所示是一种过山车的简易模型，它由水平轨道和在竖直平面内的三个圆形轨道组成，B、C、D分别是三个圆形轨道的最低点，B、C间距与C、D间距相等，半径R1=2.0m、R2=1.4m．一个质量为m=1.0kg的小球（视为质点），从轨道的左侧A点以v0=12.0m/s的初速度沿轨道向右运动，A、B间距L1=6.0m．小球与水平轨道间的动摩擦因数μ=0.2，圆形轨道是光滑的．假设水平轨道足够长，圆形轨道间不相互重叠．重力加速度取g=10m/s2，计算结果保留小数点后一位数字．试求：
（1）小球在经过第一个圆形轨道的最高点时，轨道对小球作用力的大小；
（2）如果小球恰能通过第二圆形轨道，B、C间距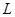
应是多少；
（3）在满足（2）的条件下，如果要使小球不能脱离轨道，在第三个圆形轨道的设计中，半径R3应满足的条件和小球最终停留点与起点间的距离．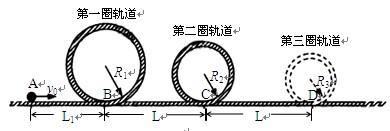
如图所示，用同种材料制成的一个轨道ABC，AB段为四分之一圆弧，半径为R=2m，BC段为水平放置的轨道。一个物块质量为m=2kg，与轨道的动摩擦因数为μ=0．25，它由轨道顶端A从静止开始下滑，恰好运动到C端停止，测得物块滑至底端B点的速度为5m/s，求：（g取10m/s2）
（1）物块在AB段克服摩擦力做功为多少？
（2）水平轨道BC段的长度为多大？
从离地面H高处落下一只小球，小球在运动过程中所受到的空气阻力是它重力的k倍，而小球与地面相碰后，能以相同大小的速率反弹，则小球从释放开始，直至停止弹跳为止，所通过的总路程为多少？
汽车在水平直线公路上行驶，额定功率为
，汽车行驶过程中所受阻力恒为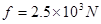
，汽车的质量
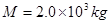。若汽车从静止开始做匀加速直线运动，加速度的大小为
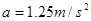，汽车达到额定功率后，保持额定功率不变继续行驶求：（1）汽车在整个运动过程中所能达到的最大速度；
（2）匀加速运动能保持多长时间；
（3）当汽车的速度为20m/s时的加速度
分）如图所示，质量为m=1kg的滑块，以ν0＝5m/s的水平初速度滑上静止在光滑水平面的平板小车，小车足够长，质量M=4kg。求：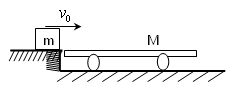
（1）滑块与小车的共同速度ν；
（2）整个运动过程中产生的内能E。
）（一定质量的理想气体从状态A变化到状态B，再变化到状态C，其状态变化过程的P-T图象如图所示。已知该气体在状态A时的体积为1×10-3m3。求：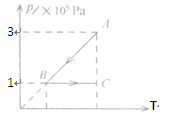
(i)该气体在状态C时的体积；
(ii)该气体从状态A到状态B再到状态c的过程中，气体与外界传递的热量