如图所示,在光滑水平面AB上,水平恒力F推动质量为m="1" kg的物体从A点由静止开始做匀加速直线运动,物体到达B点时撤去F,接着又冲上光滑斜面(设经过B点前后速度大小不变,最高能到达C点,用速度传感器测量物体的瞬时速度,表中记录了部分测量数据),求:
| t(s) |
0.0 |
0.2 |
0.4 |
… |
2.2 |
2.4 |
2.6 |
… |
| v(m/s) |
0.0 |
0.4 |
0.8 |
… |
3.0 |
2.0 |
1.0 |
… |
(1)恒力F的大小.
(2)斜面的倾角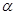 .
.
(3)t="2.1" s时物体的速度.
(15分) 一游客在峨眉山滑雪时,由静止开始沿倾角为37°的山坡匀加速滑下。下滑过程中从A 点开始给游客抓拍一张连续曝光的照片如图所示。经测量游客从起点到本次曝光的中间时刻的位移恰好是40m。已知本次摄影的曝光时间是0.2s ,照片中虚影的长度L 相当于实际长度4m,试计算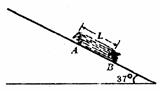
(1) 运动员下滑的加速度
(2)滑雪板与坡道间的动摩擦因数。( g=10m/s2 , sin370=0.6 , cos370=0.8 ) (保留两位有效数字)
在赛车场上,为了安全起见,车道外围都固定上废旧轮胎作为围栏,当车碰撞围拦时起缓冲器作用.为了检验废旧轮胎的缓冲效果,在一次模拟实验中用弹簧来代替废旧轮胎,实验情况如图所示.水平放置的轻弹簧左侧固定于墙上,处于自然状态,开始赛车在A处处于静止,距弹簧自由端的距离为L1=1m。当赛车起动时,产生水平向左的牵引力恒为F=24N使赛车向左做匀加速前进,当赛车接触弹簧的瞬间立即关闭发动机撤去F,赛车继续压缩弹簧,最后被弹回到B处停下.已知赛车的质量为m=2kg,A、B之间的距离为L2=3m,赛车被弹回的过程中离开弹簧时的速度大小为v=4m/s,水平向右.g=10m/s2求: 
(1)赛车和地面间的动摩擦因数;
(2)弹簧被压缩的最大距离;
(3)弹簧的最大弹性势能。
(12分)如图所示,质量为M的小球被一根长为L=0.7米的可绕O轴自由转动的轻质杆固定在其端点,同时又通过绳跨过光滑定滑轮与质量为m的小球相连.若将质量为M="3" 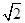 m的球由杆呈水平状态开始释放,不计摩擦,竖直绳足够长,则当杆转动到竖直位置时,质量为m的球的速度是多大?g=10m/s2
m的球由杆呈水平状态开始释放,不计摩擦,竖直绳足够长,则当杆转动到竖直位置时,质量为m的球的速度是多大?g=10m/s2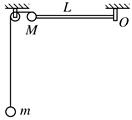
(12分)如图所示为两组平行板金属板,一组竖直放置,一组水平放置,今有一质量为m的电子静止在竖直放置的平行金属板的A点,经电压U0加速后通过B点进入两板间距为d、电压为U的水平放置的平行金属板间,若电子从两块水平平行板的正中间射入,且最后电子刚好能从右侧的两块平行金属板穿出,A、B分别为两块竖直板的中点,求: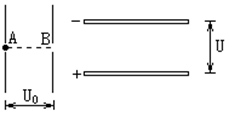
(1)电子通过B点时的速度大小;
(2)右侧平行金属板的长度;
(3)电子穿出右侧平行金属板时的动能。
一列货车的质量为5.0×105kg,在平直轨道以额定功率3000kw加速行驶,当速度由10m/s加速到所能达到的最大速度30m/s时,共用了2min,则这段时间内列车前进的距离是多少?g=10m/s2