如图,在正方形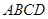 中,
中,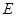 是
是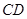 边上的中点,
边上的中点,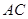 与
与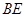 相交于点
相交于点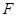 ,连接
,连接 .(注:正方形的四边相等,四个角都是直角,每一条对角线平分一组对角).
.(注:正方形的四边相等,四个角都是直角,每一条对角线平分一组对角).
(1) 在不增加点和线的前提下,直接写出图中所有的全等三角形.(不要求证明)
(2) 连接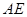 试判断
试判断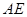 与
与 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
(3)延长 交
交 于点
于点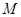 ,试判断
,试判断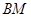 与
与 的数量关系,并说明理由.
的数量关系,并说明理由.
数学家鲁弗斯设计了一个仪器,它可以三等分一个角.如图所示,A、B、C、D分别固定在以O为公共端点的四根木条上,且OA=OB=OC=OD,E、F可以在中间的两根木条上滑动,AE=CE=BF=DF.求证:∠AOE=∠EOF=∠FOD.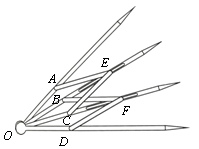
已知:如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.求证:△ABC≌△DEF.
有这样的一个定理:夹在两条平行线间的平行线段相等.下面经历探索与应用的过程.
探索:
已知:如图1,AD∥BC,AB∥CD.求证:AB=CD.
应用此定理进行证明求解.
应用一、已知:如图2,AD∥BC,AD<BC,AB=CD.求证:∠B=∠C;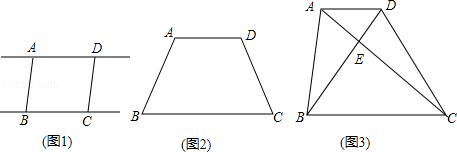
应用二、已知:如图3,AD∥BC,AC⊥BD,AC=4,BD=3.求:AD与BC两条线段的和.
如图1,四边形OABC中,OA=a,OC=3,BC=2,∠AOC=∠BCO=90°,经过点O的直线l将四边形分成两部分,直线l与
OC所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处(如图1).
(1)若折叠后点D恰为AB的中点(如图2),则θ= ;
(2)若θ=45°,四边形OABC的直角∠OCB沿直线l折叠后,点B落在点四边形OABC的边AB上的E处(如图3),求a的值.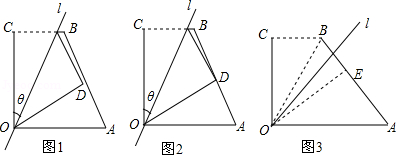
如图,在△ABC中,AB=17,BC=16,BC边上的中线AD=15,
(1)求AC;
(2)若点P在边AC上移动,则BP的最小值是 .