如图,直三棱柱 中,
中,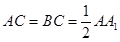 ,
,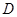 是棱
是棱 的中点,
的中点,
(1) 证明: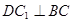
(2)求二面角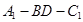 的大小. (12分)
的大小. (12分) 
(本小题满分15分)
某汽车生产企业上年度生产一品牌汽车的投入成本为10万元/辆,出厂价为13万元/辆,年销售量为5000辆.本年度为适应市场需求,计划提高产品档次,适当 增加投入成本,若每辆车投入成本增加的比例为
增加投入成本,若每辆车投入成本增加的比例为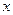 (0<
(0<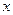 <1
<1 ,则出厂价相应提高的比例为0.7
,则出厂价相应提高的比例为0.7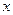 ,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量
,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量
(1)若年销售量增加的比例为0.4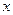 ,为使本年度的年利润比上年度有所增加,则投入成本增加的比例
,为使本年度的年利润比上年度有所增加,则投入成本增加的比例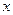 应在什么范围内?
应在什么范围内?
(2)年销售量关于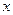 的函数为
的函数为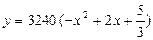 ,则当
,则当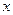 为何值时,本年度的年利润最大?最大利润为多少
为何值时,本年度的年利润最大?最大利润为多少
(本小题满分15分)
设函数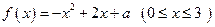 的最大值为
的最大值为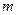 ,最小值为
,最小值为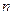 ,其中
,其中 .
.
(1)求 的值(用
的值(用 表示);
表示);
(2)已知角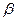
 的顶点与平面直角坐标系
的顶点与平面直角坐标系 中的原点
中的原点 重合,始边与
重合,始边与 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点 .求
.求 的值.
的值.
(本小题满分14分)
在棱长均为4的三棱柱 中,
中, 、
、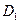 分别是BC和
分别是BC和 的中点.
的中点.
(1)求证: ∥平面
∥平面 ;
;
(2)若平面ABC⊥平面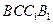 ,
, ,
,
求三棱锥 的体积.
的体积.
(本小题满分14分)
已知函数
(1)求 的值;
的值;
(2)设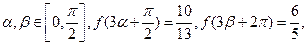 求
求 的值.
的值.
