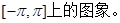某校为了解学生的学科学习兴趣,对初高中学生做了一个喜欢数学和喜欢语文的抽样调查,随机抽取了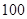 名学生,相关的数据如下表所示:
名学生,相关的数据如下表所示:
| |
数学 |
语文 |
总计 |
| 初中 |
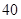 |
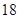 |
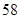 |
| 高中 |
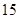 |
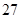 |
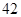 |
| 总计 |
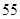 |
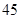 |
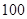 |
(1) 用分层抽样的方法从喜欢语文的学生中随机抽取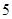 名,高中学生应该抽取几名?
名,高中学生应该抽取几名?
(2) 在(1)中抽取的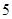 名学生中任取
名学生中任取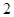 名,求恰有
名,求恰有 名初中学生的概率.
名初中学生的概率.
已知直线L的参数方程{ ,(t为参数)圆C的极坐标方程是
,(t为参数)圆C的极坐标方程是

试判断直线L与圆C的位置关系.
甲、乙、丙三人各进行一次射击,如果三人击中目标的概率都是0.6,求⑴三人都击中目标的概率;⑵其中恰有两人击中目标的概率;⑶至少有一人击中目标的概率.
如图用n种不同颜色,给图中A、B、C、D、四块区域涂色,允许同一种颜色
涂不同区域,但相邻区域不能涂同一种颜色⑴n=3,共有多少种不同的涂法?
⑵n=5,共有多少种不同的涂法?
在20件产品中,有15件正品,5件次品.从中任取3件
⑴三件中恰有一件次品的概率
⑵三件中至少有一件次品的概率
函数的性质通常指函数的定义域、值域、周期性、单调性、奇偶性等,请选择适当的探究顺序,研究函数f(x)=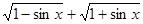 的性质,并在此基础上,作出其在
的性质,并在此基础上,作出其在