已知椭圆的中点在原点且过点 ,焦点在坐标轴上,长轴长是短轴长的3倍,求该椭圆的方程.
,焦点在坐标轴上,长轴长是短轴长的3倍,求该椭圆的方程.
已知圆C的圆心在坐标原点,且过点M(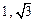 ).
).
(1)求圆C的方程;
(2)已知点P是圆C上的动点,试求点P到直线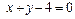 的距离的最小值;
的距离的最小值;
(3)若直线l与圆C相切,且l与x,y轴的正半轴分别相交于A,B两点,求△ABC的面积最小时直线
l的方程.
已知数列{an}中,a1="1" ,a2=3,且点(n,an)满足函数y = kx + b.
(1)求k,b的值,并写出数列{an}的通项公式;
(2)记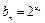 ,求数列{bn}的前n和Sn.
,求数列{bn}的前n和Sn.
如图,已知三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,AB=BC,∠ABC=90°,D为AC中点.
(1)求证:BD⊥AC1 ;
(2)若AB=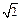 ,AA1=
,AA1=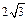 ,求AC1与平面ABC所成的角.
,求AC1与平面ABC所成的角.
 |
已知函数 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)将函数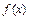 的图像上所有的点向右平移
的图像上所有的点向右平移 个单位,得到函数
个单位,得到函数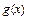 的图像,写出
的图像,写出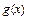 的解析式,
的解析式,
并求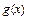 在x∈(0,π)上的单调递增区间.
在x∈(0,π)上的单调递增区间.
某市为了保障民生,防止居民住房价格过快增长,计划出台合理的房价调控政策,为此有关部门抽样调查了100个楼盘的住房销售价格,右表是这100个楼盘住房销售均价(单位:千元/平米)的频率分布表,根据右表回答以下问题:
(1)求右表中a,b的值;
(2)请将下面的频率分布直方图补充完整,并根据直方图估计该市居民住房销售价格在4千元/平米
到8千元/平米之间的概率.
| 分组 |
频数 |
频率 |
| [2,3) |
5 |
0.05 |
| [3,4) |
10 |
0.10 |
| [4,5) |
a |
0.15 |
| [5,6) |
24 |
0.24 |
| [6,7) |
18 |
0.18 |
| [7,8) |
12 |
b |
| [8,9) |
8 |
0.08 |
| [9,10) |
8 |
0.08 |
| 合计 |
100 |
1.00 |