本小题12分)命题p: 函数y= 在(-1, +
在(-1, + )上单调递增, 命题
)上单调递增, 命题 函数y=lg[
函数y=lg[ ]的定义域为R
]的定义域为R
(1) 若“ 或
或 ”为真命题,求
”为真命题,求 的取值范围;
的取值范围;
(2) 若“ 或
或 ”为真命题,“
”为真命题,“ 且
且 ”为假命题,求
”为假命题,求 的取值范围
的取值范围
 的外接圆半径
的外接圆半径 ,角
,角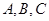 的对边分别是
的对边分别是 ,且
,且 .
.
(1)求角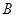 和边长
和边长 ;
;
(2)求 的最大值及取得最大值时的
的最大值及取得最大值时的 的值,并判断此时三角形的形状.
的值,并判断此时三角形的形状.
已知函数
(Ⅰ)求不等式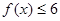 的解集;
的解集;
(Ⅱ)若关于x的不等式 的解集非空,求实数
的解集非空,求实数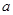 的取值范围.
的取值范围.
已知函数 .
.
(1)若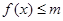 的解集为
的解集为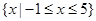 ,求实数
,求实数 的值.
的值.
(2)当 且
且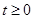 时,解关于
时,解关于 的不等式
的不等式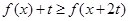 .
.
如图,已知⊙O的半径为1,MN是⊙O的直径,过M点作⊙O的切线AM,C是AM的中点,AN交⊙O于B点,若四边形BCON是平行四边形.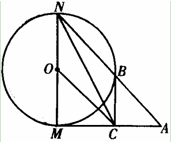
(Ⅰ)求AM的长;
(Ⅱ)求sin∠ANC.
已知函数f(x)=alnx+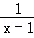 (a≠0)在(0,
(a≠0)在(0, )内有极值.
)内有极值.
(I)求实数a的取值范围;
(II)若x1∈(0, ),x2∈(2,+∞)且a∈[
),x2∈(2,+∞)且a∈[ ,2]时,求证:f(x2)﹣f(x1)≥ln2+
,2]时,求证:f(x2)﹣f(x1)≥ln2+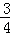 .
.