(本小题13分)曲线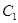 上任意一点M满足
上任意一点M满足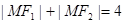 , 其中F
, 其中F (-
(-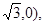 F
F (
(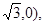 抛物线
抛物线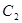 的焦点是直线y=x-1与x轴的交点, 顶点为原点O.
的焦点是直线y=x-1与x轴的交点, 顶点为原点O.
(1)求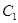 ,
,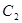 的标准方程;
的标准方程;
(2)请问是否存在直线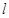 满足条件:①过
满足条件:①过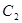 的焦点
的焦点 ;②与
;②与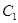 交于不同
交于不同
两点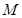 ,
, ,且满足
,且满足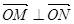 ?若存在,求出直线
?若存在,求出直线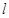 的方程;若不
的方程;若不
存在,说明理由.
(本小题满分10分)选修4-5:不等式选讲
已知函数f(x)=|x-1|
(I )解关于x;的不等式f(x)+x2-1>0;
(II )若f(x)=-|x+3|m,f(x)<g(x)的解集非空,求实数m的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,以坐标原点O为极点x轴的正半轴为极轴建立极坐标系, 曲线C1的极坐标方程为:
(I)求曲线C1的普通方程;
(II)曲线C2的方程为 ,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值.
,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值.
(本小题满分10分)选修4-1几何证明选讲
如图,AB是 O的直径,BE为圆0的切线,点c为
O的直径,BE为圆0的切线,点c为 o 上不同于A、B的一点,AD为
o 上不同于A、B的一点,AD为 的平分线,且分别与BC 交于H,与
的平分线,且分别与BC 交于H,与 O交于D,与BE交于E,连结BD、CD.
O交于D,与BE交于E,连结BD、CD.
(I )求证:BD平分
(II)求证:AH.BH=AE.HC
.(本小题满分12分)
已知函數f(x)=ln+mx2(m∈R)
(I)求函数f(x)的单调区间;
(II)若m=0,A(a,f(a))、B(b,f(b))是函数f(x)图象上不同的两点,且a>b>0,  为f(x)的导函数,求证:
为f(x)的导函数,求证:
(III)求证 
(本小题满分12分)
已知直线l1:4x:-3y+6=0和直线l2x=-p/2:.若拋物线C:y2=2px上的点到直线l1和直线l2的距离之和的最小值为2.
(I )求抛物线C的方程;
(II)若以拋物线上任意一点M为切点的直线l与直线l2交于点N,试问在x轴上是否存 在定点Q,使Q点在以MN为直径的圆上,若存在,求出点Q的坐标,若不存在,请说明理由.