若实数 、
、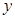 、
、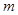 满足
满足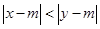 ,则称
,则称 比
比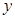 接近
接近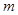 .
.
(1)若 比3接近0,求
比3接近0,求 的取值范围;
的取值范围;
(2)对任意两个不相等的正数 、
、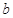 ,证明:
,证明: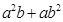 比
比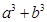 接近
接近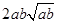 ;
;
(3)已知函数 的定义域
的定义域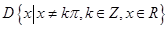 .任取
.任取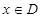 ,
, 等于
等于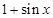 和
和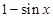 中接近0的那个值.写出函数
中接近0的那个值.写出函数 的解析式及最小值(结论不要求证明)
的解析式及最小值(结论不要求证明)
(本小题满分12分)已知函数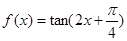 .
.
(1)求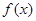 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(2)设 ,若
,若 求
求 的大小.
的大小.
已知函数f(x)满足2f(x+2)=f(x),当x∈(0,2)时,f(x)=lnx+ax ( ),当x∈(―4,―2)时,f(x)的最大值为―4.
),当x∈(―4,―2)时,f(x)的最大值为―4.
(1)求x∈(0,2)时,f(x)的解析式;
(2)是否存在实数b使得不等式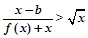 对于
对于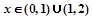 恒成立?若存在,求出实数b的取值集合;若不存在,请说明理由.
恒成立?若存在,求出实数b的取值集合;若不存在,请说明理由.
已知数列{an}满足a1=1,a2=3,且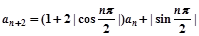 ,
, .
.
(1)证明:数列{a2k}(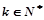 )为等比数列;
)为等比数列;
(2)求数列{an}的通项公式;
(3)设 (λ为非零整数).试确定λ的值,使得对任意
(λ为非零整数).试确定λ的值,使得对任意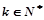 都有
都有 成立.
成立.
已知函数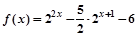 .
.
(1)当x∈[0,4]时,求f(x)的最大值和最小值;
(2)若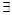 x∈[0,4],使
x∈[0,4],使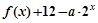 ≥0成立,求实数a的取值范围.
≥0成立,求实数a的取值范围.
某校为进行爱国主义教育,在全校组织了一次有关钓鱼岛历史知识的竞赛.现有甲、乙两队参加钓鱼岛知识竞赛,每队3人,规定每人回答一个问题,答对为本队赢得1分,答错得0分.假设甲队中每人答对的概率均为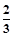 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为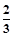 、
、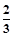 、
、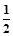 ,且各人回答正确与否相互之间没有影响,用ξ表示甲队的总得分.
,且各人回答正确与否相互之间没有影响,用ξ表示甲队的总得分.
(1)求随机变量ξ的分布列和数学期望;
(2)用A表示“甲、乙两个队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分” 这一事件,求P(AB).