在□ABCD中,E、F分别为对角线BD上的两点,且BE=DF。
(1)试说明四边形AECF是平行四边形;
(2)连结AC,当BD与AC满足 时,四边形AECF是菱形,并说明理由。 
甲、乙两同学只有一张乒乓球比赛的门票,谁都想去,最后商定通过转盘游戏决定.游戏规则是:转动下面平均分成三个扇形且标有不同颜色的转盘,转盘连续转动两次,若指针前后所指颜色相同,则甲去;否则乙去.(如果指针恰好停在分割线上,那么重转一次,直到指针指向一种颜色为止)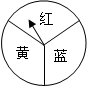
(1)转盘连续转动两次,指针所指颜色共有几种情况?通过画树状图或列表法加以说明;
(2)你认为这个游戏公平吗?请说明理由.
将一副三角尺如图①摆放(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△DEF中,∠EDF=90°,∠E=45°)点D为AB的中点,DE交AC于点P,DF经过点C.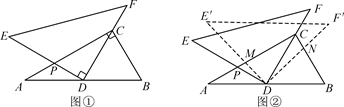
(1)求∠ADE的度数;
(2)如图②,将△DEF绕点D顺时针方向旋转角α(0°<α<60°),此时的等腰直角三角尺记为△DE′F′,DE′交AC于点M,DF′交BC于点N,试判断 的值是否随着α的变化而变化?如果不变,请求出
的值是否随着α的变化而变化?如果不变,请求出 的值;反之,请说明理由.
的值;反之,请说明理由.
某市某楼盘准备以每平方米6 000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4 860元的均价开盘销售.
(1)求平均每次下调的百分率.
(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?
如图,一次函数 的图象与反比例函数
的图象与反比例函数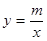 的图象交于P(-2,1)、Q(1,
的图象交于P(-2,1)、Q(1,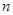 )两点.
)两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出一次函数的值大于反比例函数的值的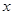 的取值范围.
的取值范围.
如图,已知菱形ABCD,AB=AC,点E,F分别是BC,AD的中点,连接AE,CF.
(1)求证:四边形AECF是矩形;
(2)若AB=8,求菱形的面积.