用代入法解方程组: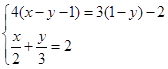
运送29.5吨煤,先用一辆载重4吨的汽车运3次,剩下的用一辆载重为2.5吨的货车运。还要运几次才能完?
2.分解因式:(3x+2y)2﹣(2x+3y)2.
解方程:9(x+1)2﹣(3x﹣5)(3x+5)=16;
某人去水果批发市场采购苹果,他看中了A、B两家苹果.这两家苹果品质一样,零售价都为6元/千克,批发价各不相同.
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠.
B家的批发价格采用分段计算方法,规定如下表:
| 数量范围 (千克) |
不超过500 |
超过500但不超过1500部分 |
超过1500但不超过2500部分 |
超过2500部分 |
| 价格 (元) |
零售价的95% |
零售价的85% |
零售价的75% |
零售价的70% |
B家示例:某人批发苹果2100千克,
则总费用为6×95%×500+6×85%×1000+6×75%×600元.
(1)如果他批发600千克苹果,则他在A 家批发需要 元,在B家批发需
要元;
(2)如果他批发x千克苹果(1500<x<2000),则他在A 家批发需要 元,在B家批发需要元(用含x的代数式表示);
(3)现在他要批发1800千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.
出租车司机小王某天下午营运全是在东西走向的太湖大道上进行的.如果向东记作“+”,向西记作“-”.他这天下午行车情况如下:(单位:千米)
-2,+5,-1,+10,-3,-2,-5,+6
请回答:
(1)小王将最后一名乘客送到目的地时,小王在下午出车的出发地的什么方向?距下午出车的出发地多远?
(2)若规定每趟车的起步价是10元,且每趟车3千米以内(含3千米)只收起步价;若超过3千米,除收起步价外,超过的每千米还需收2元钱.那么小王这天下午共收到多少钱?