已知某星球的半径为R，有一距星球表面高度h=R处的卫星，绕该星球做匀速圆周运动，测得其周期T=2π
。
求：（1）该星球表面的重力加速度g
（2）若在该星球表面有一如图所示的装置，其中AB部分为一长为12.8m并以5m/s速度顺时针匀速转动的传送带，BCD部分为一半径为1.6m竖直放置的光滑半圆形轨道，直径BD恰好竖直，并与传送带相切于B点。现将一质量为0.1kg的可视为质点的小滑块无初速地放在传送带的左端A点上，已知滑块与传送带间的动摩擦因数为0.5。
试求出到达D点时对轨道的压力大小；
(提示：
=3.2）
（1）在同一地点有两个静止的声源，发出声波1和声波2在同一空间的空气中沿同一方向传播，如图1所示为某时刻这两列波的图像，则下列说法中正确的是
| A．波1速度比波2速度大 |
| B．相对于同一障碍物，波2比波1更容易发生衍射现象 |
| C．这两列波传播的方向上，不会产生稳定的干涉现象 |
| D．这两列波传播的方向上运动的观察者，听到的这两列波的频率均与从声源发出时的频率相同 |
（2）如图2所示是一透明的圆柱体的横截面，其半径为
，折射率是
，AB是一条直径。今有一束平行光沿AB方向射向圆柱体，试求离AB多远的入射光线经折射后经过B点？
（1）如图1所示气缸内密封的气体（可视为理想气体），在等压膨胀过程中，下列关于气体说法正确的是
| A．气体内能可能减少 |
| B．气体会向外界放热 |
| C．气体吸收热量大于对外界所做的功 |
| D．气体平均动能将减小 |
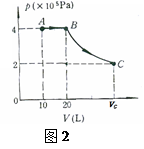
（2）一定质量的理想气体，由状态A经过等压变化到状态B，再经过等温变化到状态C，如图2所示，已知气体在状态A的温度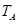
=300K。求气体在状态B的温度
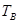和在状态C的体积
。
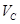为了获得一束速度大小确定且方向平行的电子流，某人设计了一种实验装置，其截面图如题9图所示。其中EABCD为一接地的金属外壳。在A处有一粒子源，可以同时向平行于纸面的各个方向射出大量的速率不等的电子。忽略电子间的相互作用力，这些电子进入一垂直于纸面向里的圆形区域匀强磁场后，仅有一部分能进入右侧的速度选择器MNPQ。已知圆形磁场半径为R；速度选择器的MN和PQ板都足够长，板间电场强度为E（图中未画出电场线），匀强磁场垂直于纸面向里大小为B2，电子的电荷量大小为e，质量为m。调节圆形区域磁场的磁感应强度B1的大小，直到有电子从速度选择器右侧射出。求：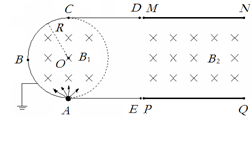
（1）速度选择器的MN板带正电还是负电？能从速度选择器右侧射出的电子的速度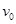
大小、方向如何？
（2）是否所有从粒子源A处射出并进入磁场的速度大小为（1）问中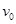的电子，最终都能从速度选择器右侧射出？若能，请简要证明，并求出圆形磁场的磁感应强度B1的大小；若不能，请说明理由。（不考虑电子“擦”到金属板的情形以及金属板附近的边界效应）
（3）在最终能通过速度选择器的电子中，从圆形区域磁场出射时距AE为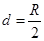
的电子在圆形磁场中运动了多长时间？
如图1所示，一质量为m的滑块（可视为质点）沿某斜面顶端A由静止滑下，已知滑块与斜面间的动摩擦因数
和滑块到斜面顶端的距离
的关系如图2所示。斜面倾角为37°，长为L。有一半径
的光滑竖直半圆轨道刚好与斜面底端B相接，且直径BC与水平面垂直，假设滑块经过B点时没有能量损失。当滑块运动到斜面底端B又与质量为m的静止小球（可视为质点）发生弹性碰撞（已知：
，
）。求：
（1）滑块滑至斜面底端B时的速度大小；
（2）在B点小球与滑块碰撞后小球的速度大小；
（3）滑块滑至光滑竖直半圆轨道的最高点C时对轨道的压力。
某同学做了用吹风机吹物体前进的一组实验，吹风机随物体一起前进时，让出气口与该物体始终保持恒定距离，以确保每次吹风过程中吹风机对物体施加的水平风力保持恒定。设物体A和物体B的质量关系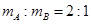
。在水平桌面上画等距的三条平行于桌子边缘的直线1、2、3，如图所示。空气和桌面对物体的阻力均忽略不计。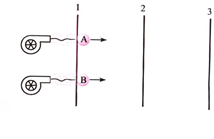
（1）用同一吹风机将物体按上述要求吹动A、B两物体时，获得的加速度之比；
（2）用同一吹风机将物体A从第1条线由静止吹到第2条线，又将物体B从第1条线由静止吹到第3条线。求这两次A、B物体获得的速度之比。