已知函数 在点
在点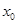 处取得极大值
处取得极大值  ,其导函数
,其导函数 的图象经过点
的图象经过点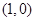 ,
,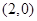 ,如图所示.求:
,如图所示.求: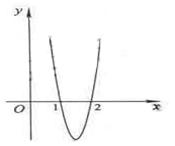
(Ⅰ)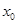 的值;
的值;
(Ⅱ)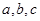 的值.
的值.
飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔20250m,速度为1000km/h,飞行员先看到山顶的俯角为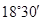 ,经过150s后又看到山顶的俯角为
,经过150s后又看到山顶的俯角为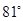 ,求山顶的海拔高度(精确到1m).
,求山顶的海拔高度(精确到1m).
一架飞以326km/h的速度,沿北偏东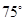 的航向从城市A出发向城市B飞行,18min以后,飞机由于天气原因按命令改飞另一个城市C,问收到命令时飞机应该沿什么航向飞行,此时离城市C的距离是多少?
的航向从城市A出发向城市B飞行,18min以后,飞机由于天气原因按命令改飞另一个城市C,问收到命令时飞机应该沿什么航向飞行,此时离城市C的距离是多少?
A,B两地相距2558m,从A,B两处发出的两束探照灯光照射在上方一架飞机的机身上(如图),飞机离两个探照灯的距离是多少?飞机的高度是多少?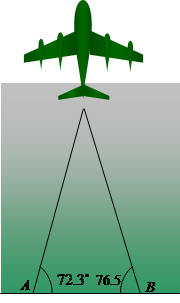
为测量某塔的高度,在A,B两点进行测量的数据如图所示,求塔的高度.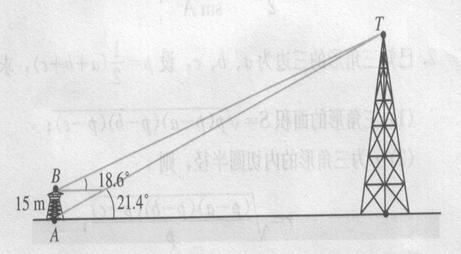
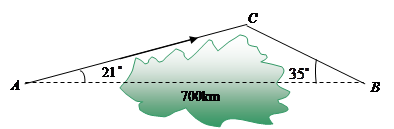
一架飞机从A地飞到B到,两地相距700km.飞行员为了避开某一区域的雷雨云层,从机场起飞后,就沿与原来的飞行方向成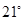 角的方向飞行,飞行到中途,再沿与原来的飞行方向成
角的方向飞行,飞行到中途,再沿与原来的飞行方向成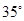 夹角的方向继续飞行直到终点.这样飞机的飞行路程比原来路程700km远了多少?
夹角的方向继续飞行直到终点.这样飞机的飞行路程比原来路程700km远了多少?