下面是一城市某日的气温变化图,在这个图中可以看出很多温度变化的信息.例如:这一天的最高气温是14°.请你另外指出3条图中所反映的信息.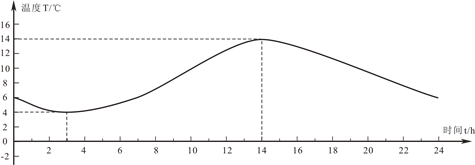
抛物线 经过点A(4,0),B(2,2),连结OB,AB.
经过点A(4,0),B(2,2),连结OB,AB.
(1)求 、
、 的值;
的值;
(2)求证:△OAB是等腰直角三角形;
(3)将△OAB绕点O按顺时针方向旋转l35°得到△OA′B′,写出A′B′的中点P的出标.试判断点P是否在此抛物线上,并说明理由.
某旅游商店8月份营业额为15万元,9月份下降了20%.受“十一”黄金周以及经济利好因素的影响,10月份、11月份营业额均比上一个月有所增长,10月份增长率是11月份增长率的1.5倍,已知该旅游商店11月份营业额为24万元.
(1)问:9月份的营业额是多少万元?
(2)求10月份营业额的增长率.
如图,在梯形ABCD中,AB∥CD,∠DAB=90°,AC⊥BC.
(1)求证:△ADC∽△BCA;
(2)若AB=9cm,AC=6cm,求梯形ABCD中位线的长度.
以直线 为对称轴的抛物线
为对称轴的抛物线 与
与 轴交于A、B两点,其中点A的坐标为
轴交于A、B两点,其中点A的坐标为 .
.
(1)求点B的坐标;
(2)设点M 、N
、N 在抛物线线上,且
在抛物线线上,且 ,试比较
,试比较 、
、 的大小.
的大小.
一只不透明的箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同.
(1)从箱子中随机摸出一个球是白球的概率是多少?
(2)从箱子中随机摸出一个球,记录下颜色后不将它放回箱子,搅匀后再摸出一个球,请你用列表或画出树状图的方法,求出两次摸出的球都是白球的概率.