在直角坐标系中，已知抛物线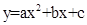
与x轴交于点A(1，0)和点B，顶点为P.
(1)若点P的坐标为（－1，4），求此时抛物线的解析式；
（2）如图若点P的坐标为（－1，k）,k＜0，点Q是y轴上一个动点，
当k为何值时，QB＋QP取得最小值为5；
（3）试求满足（2）时动点Q的坐标. （本题12分）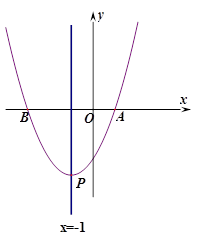
已知：如图，∠B=90°，AB∥DF，AB=3cm，BD=8cm，点C是线段BD上一动点，点E是直线DF上一动点，且始终保持AC⊥CE．
（1）试说明：∠ACB =∠CED
（2）若AC="CE" ，试求DE的长
（3）在线段BD的延长线上，是否存在点C，使得AC=CE，若存在，请求出DE的长及△AEC的面积；若不存在，请说明理由。
如图，在直角坐标系中，Rt△AOB的两条直角边OA，OB分别在x轴的负半轴，y轴的负半轴上，且OA=2，OB=1．将Rt△AOB绕点O按顺时针方向旋转90°，再把所得的像沿x轴正方向平移1个单位，得△CDO．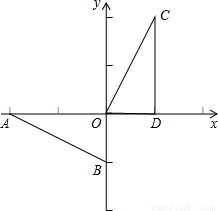
（1）写出点A，B，C，D的坐标；
（2）求点A和点C之间的距离
如图，长方体的底面是边长为1cm 的正方形，高为3cm．
（1）如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B，请计算所用细线最短需要cm？
（2）如果从点A开始经过4个侧面缠绕3圈到达点B，那么所用细线最短需要 cm．（直接填空）
如图，点B、F、C、E在一条直线上，BF=EC，AB∥ED，AC∥FD，求证：AC=DF．
如图：在8
8的正方形网格中，已知网格中小正方形的边长为1， 
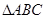的三个顶点在格点上。
（1）画出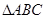关于直线
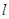的对称图形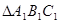
；
（2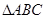）_____________直角三角形（填“是”或“不是”
（3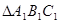）的面积是_____________