在平面直角坐标系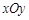 中,对于任意两点
中,对于任意两点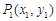 与
与 的“非常距离”,给出如下定义:
的“非常距离”,给出如下定义:
若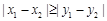 ,则点
,则点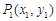 与点
与点 的非常距离为
的非常距离为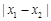 ;
;
若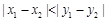 ,则点
,则点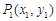 与点
与点 的非常距离为
的非常距离为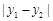 ;
;
例如:点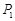 (1,2),点
(1,2),点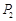 (3,5),因为
(3,5),因为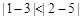 ,所以点
,所以点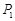 与点
与点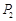 的“非常距离”为
的“非常距离”为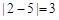 ,也就是图1中线段
,也就是图1中线段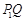 与线段
与线段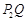 长度的较大值(点Q为垂直于y轴的直线
长度的较大值(点Q为垂直于y轴的直线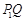 与垂直于x轴的直线
与垂直于x轴的直线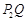 的交点).
的交点).
(1)已知点A(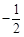 ,0),B为y轴上的一个动点,
,0),B为y轴上的一个动点,
①若点A与点B的“非常距离”为2,写出满足条件的点B的坐标;
②直接写出点A与点B的“非常距离”的最小值.
(2)已知C是直线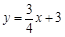 上的一个动点,
上的一个动点,
①如图2,点D的坐标是(0,1),求点C与点D的“非常距离”的最小值及相应的点C的坐标;
②如图3,E是以原点O为圆心,1为半径的圆上的一个动点,求点C与点E的“非常距离”的最小值及相应点E和点C的坐标.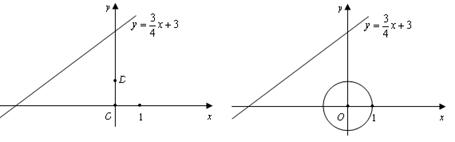
如图,在8×11的方格纸中,△ABC的顶点均在小正方形的顶点处.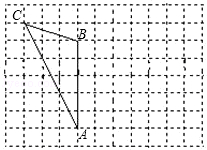
(1)画出△ABC绕点A顺时针方向旋转90°得到的△A′B′C′;
(2)求点B运动到点B′所经过的路径的长度.
如图,已知矩形ABCD的边AB=4,BC=3,按照图示位置放置在直线AP上,然后转动,当它转动一周时,求顶点A经过的路线长.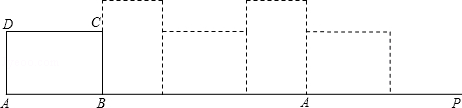
一段圆弧形公路弯道,圆弧的半径为2km,弯道所对圆心角为10°,一辆汽车从此弯道上驶过,用时20s,弯道有一块限速警示牌,限速为40km/h,问这辆汽车经过弯道时有没有超速?(π取3)
如图,在⊙O中,C﹑D为⊙O上两点,AB是⊙O的直径,已知∠AOC=130°,AB=2.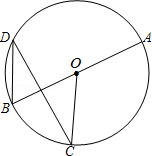
求:(1)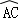 的长;
的长;
(2)∠D的度数.
如图,在⊙O中,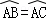 ,∠APC=60°.
,∠APC=60°.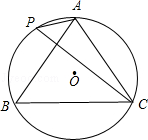
(1)求证:△ABC是等边三角形;
(2)若⊙O的半径为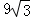 ,∠BCP=40°,求
,∠BCP=40°,求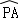 的长.
的长.