如图所示,匀强电场区域和匀强磁场区域是紧邻的,且宽度相等均为 d ,电场方向在纸平面内竖直向下,而磁场方向垂直纸面向里.一带正电粒子从 O 点以速度 v0沿垂直电场方向进入电场,在电场力的作用下发生偏转,从 A 点离开电场进入磁场,离开电场时带电粒子在电场方向的位移为电场宽度的一半,当粒子从C点穿出磁场时速度方向与进入电场O点时的速度方一致,(带电粒子重力不计)求
(l)粒子从 C 点穿出磁场时的速度v;
(2)电场强度 E 和磁感应强度 B 的比值 E / B ;
(3)粒子在电、磁场中运动的总时间。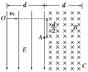
如图所示,在xOy平面内存在均匀、大小随时间周期性变化的磁场和电场,变化规律分别如图乙、丙所示(规定垂直纸面向里为磁感应强度的正方向、沿y轴正方向电场强度为正)。在t=0时刻由原点O发射初速度大小为vo,方向沿y轴正方向的带负电粒子。
已知v0、t0、B0,粒子的比荷为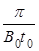 ,不计粒子的重力。求:
,不计粒子的重力。求: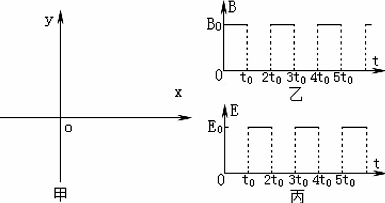
(1) t= t0时,求粒子的位置坐标;
(2)若t=5t0时粒子回到原点,求0~5to时间内粒子距x轴的最大距离;
(3)若粒子能够回到原点,求满足条件的所有E0值。
如图所示,在竖直平面内固定有两个很靠近的同心圆形轨道,外圆ABCD光滑,内圆A′B′C′D′的上半部分B′C′D′粗糙,下半部分B′A′D′光滑.一质量m=0.2 kg的小球从轨道的最低点A以初速度v0向右运动,球的尺寸略小于两圆间距,球运动的半径R=0.2 m,取g=10 m/s2.(1)若要使小球始终紧贴外圆做完整的圆周运动,初速度v0至少为多少?(2)若v0=3 m/s,经过一段时间小球到达最高点,内轨道对小球的支持力N=2 N,则小球在这段时间内克服摩擦力做的功是多少?(3)若v0=3 m/s,经过足够长的时间后,小球经过最低点A时受到的支持力为多少?小球在整个运动过程中减少的机械能是多少?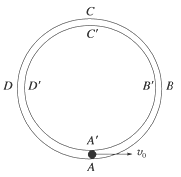
如图所示,水平面xx´上竖直放着两根两平行金属板M、N,板间距离为L=1m,两板间接一阻值为2Ω的电阻,在N板上开一小孔Q,在M、N及Q上方有向里匀强磁场B0=1T;在Nx´范围内有一450分界线连接Q和水平面,NQ与分界线间有向外的磁感应强度B=0.5T的匀强磁场;N、水平面及分界线间有竖直向上的电场;现有一质量为0.2㎏的金属棒搭在M、N之间并与MN良好接触,金属棒在MN之间的有效电阻为1Ω,M、N电阻不计,现用额定功率为P0=9瓦的机械以恒定加速度a=1m/s2匀加速启动拉着金属棒向上运动,在金属棒达最大速度后,在与Q等高并靠近M板的P点释放一个质量为m电量为+q的离子,离子的荷质比为20000C/㎏,求:
(1)金属棒匀加速运动的时间。(结果保留到小数点后一位)
(2)离子刚出Q点时的速度。
(3)离子出Q点后,在竖直向上的电场作用下,刚好能打到分界线与水平面的交点K,过K后再也不回到磁场B中,求Q到水平面的距离及离子在磁场B中的运动时间。
某同学为研究平抛运动的规律而进行了一项小测试,如图所示.薄壁圆筒半径为R,a、b是圆筒某直径上的两个端点(图中OO′为圆筒的直径).圆筒以速度v竖直匀速下落.某时刻子弹沿图示平面正好水平射入a点,且恰能经b点穿出.
(1)求子弹射入a点时速度的大小.
(2)若圆筒匀速下落的同时绕OO′匀速转动,求圆筒转动的角速度条件.
如图所示是一辆汽车从高台水平飞出后所摄得的频闪照片,照片上的虚线为用铅笔画出的正方形格子,若汽车的长度是3.6 m,取 ,求:
,求:
(1)频闪的时间间隔t;
(2)汽车离开高台时的速度.