如图1,是边长分别为5和2的两个等边三角形纸片ABC和CDˊEˊ叠放在一起.
(1)操作:固定△ABC,将△CDˊEˊ绕点C顺时针旋转得到△CDE,连结AD、BE,如图2.探究:在图2中,线段BE与AD之间有怎样的大小关系?试说明理由;
(2)操作:固定△ABC,若将△CDˊEˊ绕点C顺时针旋转30°得到△CDE,连结AD、BE,CE的延长线交AB于点F,在线段CF上沿着CF方向以每秒1个单位长的速度平移,平移后的△CDE设为△PQR,如图3.探究:在图3中,除△ABC和△PQR外,还有哪个三角形是等腰三角形?写出你的结论并说明理由;
(3)探究:如图3,在(2)的条件下,设△PQR移动的时间为1秒,求△PQR与△AFC重叠部分的面积。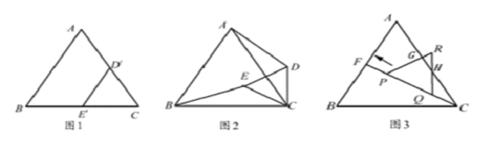
将一长方形纸片按如图的方式折叠,BC、BD为折痕,求∠CBD的度数
我们知道两条直线相交,一共有两对对顶角、4对邻补角,那么三条直线、四条直线,甚至是几条直线交于一点或两两相交有多少对对顶角和邻补角?请动手操作,观察填表,并归纳。

 ……
……
① ② ③
(1)请观察上图并填写下表:
| 图形编号 |
① |
② |
③ |
…… |
| 对顶角的对数 |
2 |
6 |
12 |
|
| 邻补角的对数 |
4 |
12 |
24 |
(2)若n条直线相交于一点,则共有多少对对顶角?共有多少对邻补角?
数学课上,老师挂出小黑板,两个三角板按如图所示的位置放置。图中有对顶角和邻补角?请你把图中所有的对顶角和邻补角都写出来。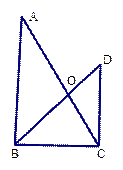
如图所示,三条直线AB、CD、EF相交于点O,∠AOF=3∠FOB,∠AOC=90°,求∠EOC的度数。
用三角尺和直尺画平行线.
(1)过点A画MN∥BC(图(1));
(2)过点P画PE∥OA,交OB于点E;画PH∥OB,交OA于点H(图(2));
(3)过点C画CE∥DA,与AB交于点E;过点C画CF∥DB,与AB的延长线交于点F(图(3)).