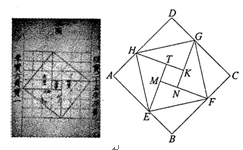
我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若S1+S2+S3=10,则S2的值是( )
| A.5 | B.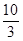 |
C.3 | D.4 |
线段AB的长为a,线段AB在投影面P上的正投影的长度为b,则a,b的大小关系是( )
| A.a>b |
| B.a=b |
| C.a<b |
| D.a≥b |
正三棱柱的正投影可能是( )
①三角形;②圆;③矩形;④线段.
| A.①③ |
| B.①③④ |
| C.③④ |
| D.①②③④ |
甲、乙两人身高相等,他们在同一路灯下影长的关系是( )
| A.一定相等 |
| B.甲的比乙的长 |
| C.乙的比甲的长 |
| D.不确定 |
下列投影图不正确的是( )
A. |
B. |
C.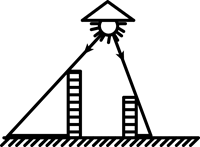 |
D.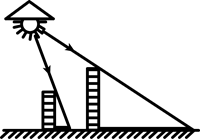 |
在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下( )
| A.小明的影子比小强的影子长 |
| B.小明的影子比小强的影子短 |
| C.小明的影子和小强的影子一样长 |
| D.无法判断谁的影子长 |