(本小题满分10分)河上有一抛物线型拱桥,当水面距拱顶5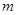 时,水面宽为8
时,水面宽为8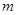 ,一小船宽4
,一小船宽4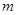 ,高2
,高2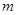 ,载货后船露出水面上的部分高
,载货后船露出水面上的部分高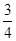
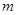 ,问水面上涨到与抛物线拱顶相距多少米时,小船恰好能通行。
,问水面上涨到与抛物线拱顶相距多少米时,小船恰好能通行。
设数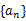 是等差数列,前n项和为
是等差数列,前n项和为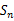 ,
, 是单调递增的等比数列,
是单调递增的等比数列,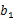 是
是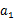 与
与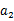 的等差中项
的等差中项 ,若当
,若当 时,
时, 恒成立,则m的最小值为.
恒成立,则m的最小值为.
如图为函数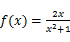 的部分图象,ABCD是矩形,A,B在图像上,将此矩形绕x轴旋转得到的旋转体的体积的最大值为
的部分图象,ABCD是矩形,A,B在图像上,将此矩形绕x轴旋转得到的旋转体的体积的最大值为
A.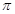 |
B.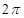 |
C. |
D. |
(本小题14分)已知函数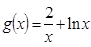 ,
, ,
, .
.
(1)求函数 的极值点;
的极值点;
(2)若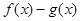 在
在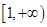 上为单调函数,求
上为单调函数,求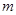 的取值范围;
的取值范围;
(3)设 ,若在
,若在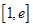 上至少存在一个
上至少存在一个 ,使得
,使得 成立,求
成立,求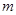 的取值范围.
的取值范围.
(本小题13分)已知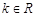 ,函数
,函数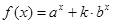
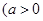 且
且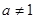 ,
, 且
且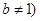 .
.
(1)如果实数 满足
满足 且
且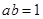 ,函数
,函数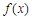 是否具有奇偶性? 如果有,求出相应的
是否具有奇偶性? 如果有,求出相应的 值;如果没有,说明原因;
值;如果没有,说明原因;
(2)如果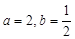 ,讨论函数
,讨论函数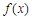 的单调性。
的单调性。
(本小题12分)已知圆C: ,其中
,其中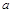 为实常数.
为实常数.
(1)若直线l: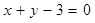 被圆C截得的弦长为2,求
被圆C截得的弦长为2,求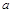 的值;
的值;
(2)设点 ,0为坐标原点,若圆C上存在点M,使|MA|="2" |MO|,求
,0为坐标原点,若圆C上存在点M,使|MA|="2" |MO|,求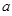 的取值范围.
的取值范围.