如图所示,均可视为质点的三个物体A、B、C穿在竖直固定的光滑绝缘轻杆上,A与B紧靠在一起(但不粘连),C紧贴着绝缘地板,质量分别为MA=2.32kg,MB=0.20kg,MC=2.00kg,其中A不带电,B、C的带电量分别为qB = +4.0×10-5c,qC =+7.0×10-5c,且电量都保持不变,开始时三个物体均静止。现给物体A施加一个竖直向上的力F,若使A由静止开始向上作加速度大小为a=4.0m/s2的匀加速直线运动,则开始需给物体A施加一个竖直向上的变力F,经时间t后, F变为恒力。已知g=10m/s2,静电力恒量k=9×109N·m2/c2,
求:(1)静止时B与C之间的距离;
(2)时间t的大小;
(3)在时间t内,若变力F做的功WF=53.36J,则B所受的电场力对B做的功为多大?
一物块在粗糙水平面上,受到的水平拉力F随时间t变化如图(a)所示,速度v随时间t变化如图(b)所示,(g=10m/s2)。求:
(1)1秒末物块所受摩擦力f的大小。
(2)物块质量m。
(3)物体与地面间的动摩擦因数
如图甲所示,质量为M=3.0kg的平板小车C静止在光滑的水平面上,在t=0时,两个质量均为1.0kg的小物体A和B同时从左右两端水平冲上小车,1.0s内它们的v-t图象如图乙所示,( g取10m/s2)求:

(1)小物体A和B与平板小车之间的动摩擦因数μA、μB
(2)判断小车在0~1.0s内所做的运动,并说明理由?
(3)要使A、B在整个运动过程中不会相碰,车的长度至少为多少?
如图所示,一粗糙斜面AB与光滑圆弧轨道BCD相切,C为圆弧轨道的最低点,圆弧BC所对圆心角θ=37°。已知圆弧轨道半径为R=0.5m,斜面AB的长度为L=2.875m。质量为m=1kg的小物块(可视为质点)从斜面顶端A点处由静止开始沿斜面下滑,从B点进入圆弧轨道运动恰能通过最高点D。sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2。求:
(1)物块经C点时对圆弧轨道的压力Fc;
(2)物块与斜面间的动摩擦因数μ。
如图所示,质量分别为M和m的两个小物块用轻绳连接,绳跨过倾角α=37°的斜面顶端的定滑轮,绳平行于斜面,滑轮与转轴之间的摩擦不计,已知M=2m=2kg。开始时,用手托物块M,使M离水平面的高度为h=0.5m,物块m静止在斜面底端。撤去手,使M和m从静止开始做匀加速直线运动,经过t=0.5s,M落到水平面上,停止运动,由于绳子松弛,之后物块m不再受到绳子的拉力作用。求:(g取10m/s2)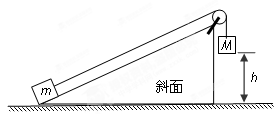
(1)物块M竖直向下运动过程加速度的大小;
(2)物块m所受到的摩擦力大小
(3)物块m沿斜面运动的最大距离?(假设斜面足够长)
如图甲所示,质量m="l" kg的物块在平行斜面向上的拉力尸作用下从静止开始沿斜面向上运动,t=0.5s时撤去拉力,利用速度传感器得到其速度随时间的变化关系图象(v-t图象)如图乙所示,g取l0m/s2,求: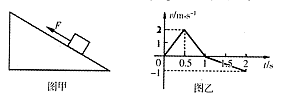
(1)2s内物块的位移大小s和通过的路程L;
(2)沿斜面向上运动两个阶段加速度大小a1、a2和拉力大小F。