某汽车租赁公司拥有20辆汽车．据统计，当每辆车的日租金为400元时，可全部租出；当每 辆车的日租金每增加50元，未租出的车将增加1辆；公司平均每日的各项支出共4800元．设公司每日租出x辆车时，日收益为y元．（日收益=日租金收入一平均每日各项支出）
（1）公司每日租出x辆车时，每辆车的日租金为 元（用含x的代数式表示）；
（2）当每日租出多少辆时，租赁公司日收益最大？最大是多少元？
（3）当每日租出多少辆时，租赁公司的日收益不盈也不亏？
如图，已知□ABCD的对角线AC、BD相交于点O，AC =12，BD=18，且△AOB的周长l=23，求AB的长．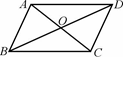
（1）计算: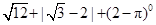
（2）解方程：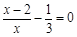
．
解方程(不等式组)
（1）
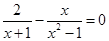
(2)
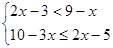
实践与探究：
对于任意正实数a、b，∵
≥0， ∴
≥0，∴
≥
只有当a＝b时，等号成立。
结论：在≥（a、b均为正实数）中，若ab为定值p，则a+b≥
，只有当a＝b时，a+b有最小值。根据上述内容，回答下列问题：
（1）若m＞0，只有当m＝时，
有最小值；
若m＞0，只有当m＝时，2
有最小值.
（2）如图，已知直线L1：
与x轴交于点A，过点A的另一直线L2与双曲线
相交于点B（2，m），求直线L2的解析式.
（3）在（2）的条件下，若点C为双曲线上任意一点，作CD∥y轴交直线L1
于点D，试求当线段CD最短时，点A、B、C、D围成的四边形面积.
如图，一次函数的图象与反比例函数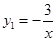
（x＜0）的图象相交于A点，与y轴、x轴分别相交于B、C两点，且C（2，0），当
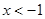时，一次函数值大于反比例函数值，当
时，一次函数值小于反比例函数值．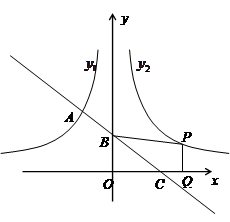
（1）求一次函数的解析式；
（2）设函数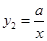
（x＞0）的图象与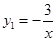（x＜0）的图象关于y轴对称，在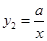（x＞0）的图象上取一点P（P点的横坐标大于2），过P点作PQ⊥x轴，垂足是Q，若四边形BCQP的面积等于2，求P点的坐标．