实践与探究：
对于任意正实数a、b，∵
≥0， ∴
≥0，∴
≥
只有当a＝b时，等号成立。
结论：在≥（a、b均为正实数）中，若ab为定值p，则a+b≥
，只有当a＝b时，a+b有最小值。 根据上述内容，回答下列问题：
（1）若m＞0，只有当m＝ 时，
有最小值 ；
若m＞0，只有当m＝ 时，2
有最小值 .
（2）如图，已知直线L1：
与x轴交于点A，过点A的另一直线L2与双曲线
相交于点B（2，m），求直线L2的解析式.
（3）在（2）的条件下，若点C为双曲线上任意一点，作CD∥y轴交直线L1
于点D，试求当线段CD最短时，点A、B、C、D围成的四边形面积.
先阅读理解下列题，再按要求完成问题：
例题：解一元二次不等式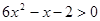
解：把
分解因式得：
又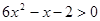所以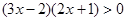
由有理数乘法法则“两数相乘，同号得正”，有
（1）
或（2）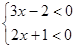
，解不等式组（1），得
解不等式（2），得
因此，一元二次不等式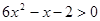的解集为或；
问题；根据阅读解不等式：
.
已知关于x的方程
解为正数，求m的取值范围.
一只箱子里共有3个球，其中2个白球，1个红球，它们除颜色外均相同。
（1）从箱子中任意摸出一个球是白球的概率是多少？
（2）从箱子中任意摸出一个球，不将它放回箱子，搅匀后再摸出一个球，求两次摸出的球都是白球的概率，并画出树状图。
甲、乙两地相距360千米。新修的高速公路开通后，在甲乙两地之间行驶的长途客运车平均车速提高了50%，而从甲地到乙地的时间缩短了2小时。试确定原来的平均车速。
利用位似图形的方法把四边形ABCD缩小为原来的
．